砺剑·2022相约高考三轮冲刺 整合卷(一)1 老高考版文科数学试题答案

砺剑·2022相约高考三轮冲刺 整合卷(一)1 老高考版文科数学试题答案,目前我们趣对答案已经整理了砺剑·2022相约高考三轮冲刺 整合卷(一)1 老高考版文科数学试题答案的各科答案和试卷,更多试卷答案请关注本趣对答案。


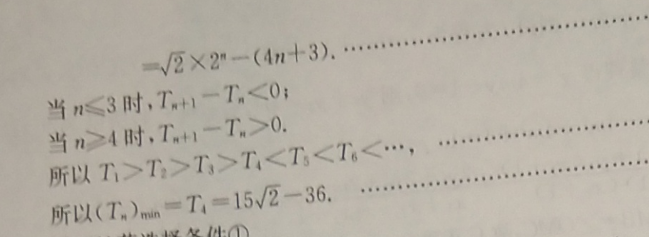
17.(1)证明:由an+1+an=2n,得an+am1=2(n-1)所以an+1-an-1=2,即数列{an}的奇数项和偶数项均为公差为2的等差数列由a1=2,a2+a1=2,得a2=32分所以a1=1+(m-1)×2=2-2=(2n=1)-2a2=2+(n-1)×2=2n-23分所以an=n-14分则an+1-an=(n+1)-2所以{an}是首项为,公差为1的等差数列5分(2)解:b2-(4n-1)=y2×2-(4n-1)6分√2、2(1-2”)_n(3+4T2(2n-1)-n(2n+1)7分Tn+1-Tn=√2(2+1-1)-(n+1)(2n+3)-2(2-1)+n(2n+1)=2×2"-(4n当n≤3时,T+1T所以T>T2>73>T

17.解:(1)a+1=2a,+3+1,可得=2,+1,设+k=(+k)…∴k,∴-k=1,k=一3,可得数列33),则数列(-3}为公比为2,首项为-2的等比数列,可得g-3=-2×(2)-1,∴a=-3×2“+3+,数列{b}的前n项和为S.满足S.=3“+c,可得S1=b1=3+c,当n≥2时,Sn-1=3-1+c,b=2×3-1,可得3+c=2×31-1,∴c=-1,可得b=2×3“-1(2)(2n-1)(9b.-2an)=(2n-1)[9×2×3-1-2(-3×2+3+1)]=(2n-1)×6×2,T=6[1×2+3×22+…+(2n-1)×2],则2T=6[1×22+3×2+…+(2m-1)×2*+1],相减可得一T=6[2+2(22+23+…+2)-(2n-1)×2+1]可得T。=12×(2n-3)×2+36.……………………………12分





