黄冈八模2022高三语文答案

黄冈八模2022高三语文答案，目前我们已经整理了黄冈八模2022高三语文答案的各科答案和试卷，更多试卷答案请关注本答案网。

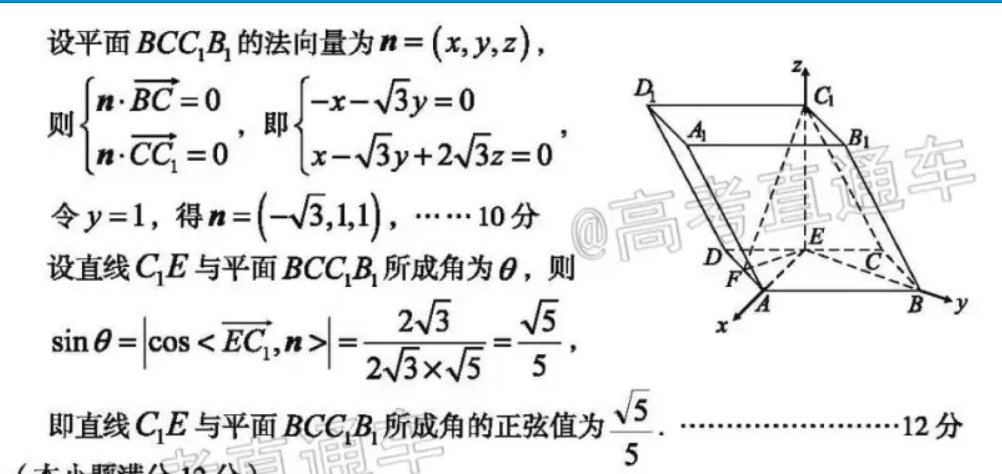
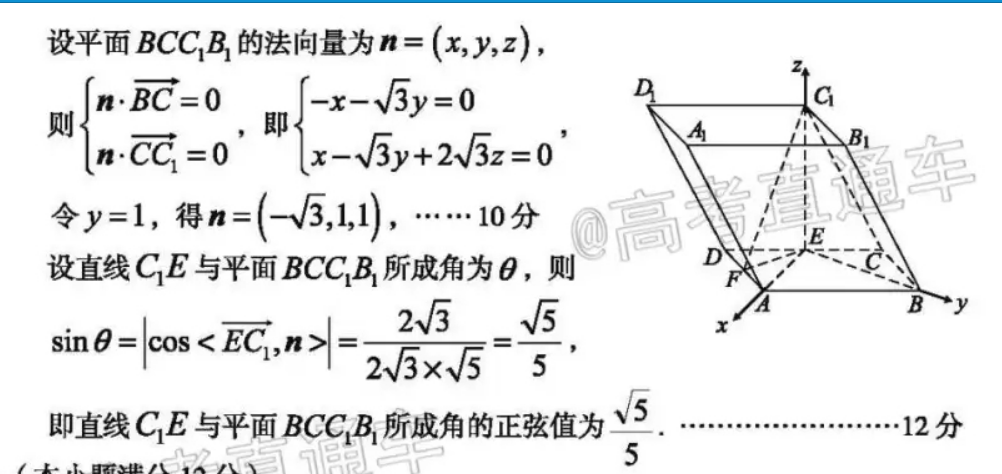
18.(本小题满分12分)(I)当点F为AD的中点时,符合题目要求分理由如下:连接FE,FC1,在△FED中,EF=√FD2+ED2-2FD,ED.c0s60°=√3,∴FD2+EF2=DE2,∴EF⊥AD.∵C1在底面上的射影E恰为CD的点,∴CE⊥平面ABCD,…………3分又ADc平面ABCD,∴CE⊥AD,且EF∩CE=E,∴AD⊥平面CEF∴点F即为所求,平面CEF即为a,此时点F为AD的中点“…“……5分(Ⅱ)连接EA,EB.在平行四边形ABCD中,∵AD=DE=EC=BC=2,∠EDA=60°,∠BCE=120∴∠CEB=30°,∠DEA=60°,∴∠AEB=90°,即EA⊥EB.分别以EA,EB,EC1为xyz轴的正方向建立空间直角坐标系如图所示,∵AB=AA=4,AD=2,易得EC1=23,则E(00)(023,0,c(025),C(-150),……7分BC(√,0),c=(,-25),B=(0023)设平面BCCB1的法向量为n=(x,y,z),n·BC=0-x-√3y=0C则即nCC,=0x-√3y+2√3z=0B令y=1,得n=(3,1),…10分设直线CE与平面BCCB所成角为日,则235sin 0=cos ECi, n>23×√55即直线CE与平面BCCB1所成角的正弦值为…12分5设平面BCCB1的法向量为n=(x,y,z),n·BC=0-x-√3y=0C则即nCC,=0x-√3y+2√3z=0B令y=1,得n=(3,1),…10分设直线CE与平面BCCB所成角为日,则235sin 0=cos ECi, n>23×√55即直线CE与平面BCCB1所成角的正弦值为…12分5

21.(本小题满分12分)(I)由题意得,f(x)=x(ax-tanx),当a=1时,f(x)=x(x-tmx),…;f(x)=x1-令g(x)=xanx,则g(x)=1--2∈0,∴g(x)在上单调递减g(0=0,:当x∈(-,0时,g(x)>0;当xe(0.元)时,g(x)<0,3分∴当x∈-2,0j时,x10, x-tanx>0f(x)>0,f(x)单调递增;当时,x1-0, x-tanx A(0)=0,f(x)=xh(x)<0,且f(x)=xh'(x)+h(x)>0重r>0即函数/在(型上单河当x∈0)时,机)<(0=0,f(x)=x(x)<0,且f(x)=功h(x)+(x)<0,f(x)<0,即函数f(x)在0.上单调递减,x=0是函数f(x)的极大值点,∴a≤1满足题意10分当a>1时,存在t∈0,。使得cost=,即h()=0,又放(x)=a-2在0上单调递减,当x∈(0)h(x)>h(0)=0f(x)=xh"(x)+h(x)>0,∴f(x)在(Q)上单调递增,这与x=0是函数f(x)的极大值点矛盾.综上所述,实数a的取值范围是(