卷临天下 全国100所名校最新高考模拟示范卷数学卷一答案

卷临天下 全国100所名校最新高考模拟示范卷数学卷一答案,目前我们已经整理了卷临天下 全国100所名校最新高考模拟示范卷数学卷一答案的各科答案和试卷,更多试卷答案请关注本答案网。






21.解:(1)解法1:由题可得,圆F的标准方程为x2+y2)2=1,即圆F的圆心为F(0,2),半径r=1.(1分)设P的坐标为(x,y),由巳知,得y+11=√x2+(y-2)2-1,(2分)易知圆F上的点均位于直线y=-1的上侧,“∴则y+1>0,所以√x2+(y-2)2=y+2.(3分)化简得曲线C的方程为x2=8y(4分)解法2:由题可得,圆F的标准方程为x2+(y-2)1,即圆F的圆心为F(0,2),半径r=1.(1分)因为C上的任意一点P到直线y=-1的距离等于该点到圆F上的点的距离的最小值,而点P到圆F上的点的距离的最小值为|PF|-rPF|-1,所以点P到点F的距离等于点P到直线y=-2的距离,(2分由抛物线的定义,可知点P的轨迹是以点F(0,2)为焦点的抛物线,(3分)所以曲线C的方程为x2=8y(4分)(2)设A(x1,y),B(x2,y2),由题意可知,直线L的斜率一定存在,故设l:y=kx十b(k≠0),kx+b联立消去y,得x2-8kx-8b=0,8y所以x1+x2=8k,x1x2=-8b,△=64k2+32b>0(6分)若向量MA+MB与向量M平行,则AMA=一kAm,by+1=-y2+1(8分)整理得yx2+x2+x1y2+x1=0,即(x1+b)x2+(kx2+b)x1+(x1+x2)=0,整理得2kx1x2+(b+1)(x1+x2)=0,即-16k+8k(b+1)=0,即8(-b+1)=0,(11分)又k≠0,所以当b=1时,上式恒成立所以直线L恒过定点,该定点为点(0,1).(12分)
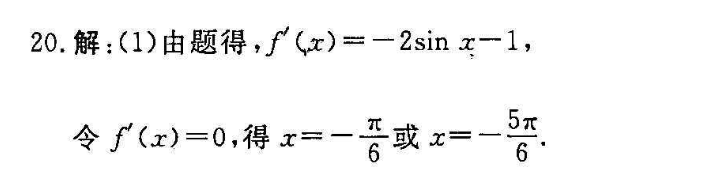





20解:(1)由题得,f(x)=-2sinx-1,令f(x)=0,得x=或兀①当x∈时,f(x)≤0,故f(x)单调递减且f(-π)=π-2>0,5x一3>0所以(2在[m一]上设有零点(3分)②当x∈[一5,一等]时,(2≥0,故f(2单调递增,且(-5)=5-3>0,(-否)=十香>0所以f(x)在57T上没有零点③当z∈[一否,x]时,f(x)≤0,故f(x)单调递减,又n)=-2-x<0,0所以()·(m)≤0所以fx)在[一,]上存在唯一的零点综上所述,函数f(x)在[一π,]上存在唯一的零点(6分)(2)若存在x∈(0,使得不等式f(x)+ax>2成立,即存在x∈(,2少使2csx+ax-x-2>0成立,设g(a)=20+x-x-2,x∈(0,2),则g(0)=0,g(2)=a-1-2inx,当x∈(0,2)时,1+2iz∈(1,3),所以g(x)∈(a-3,a-1)当a-1≤0,即a≤1时,g(x)<0,g(x)在0上单调递减,则当x∈(0,2)时,g(x)





