2022届高考北京专家信息卷 高三年级月考仿真模拟卷(7)理科数学试题答案

2022届高考北京专家信息卷 高三年级月考仿真模拟卷(7)理科数学试题答案，目前我们已经整理了2022届高考北京专家信息卷 高三年级月考仿真模拟卷(7)理科数学试题答案的各科答案和试卷，更多试卷答案请关注本答案网。

19.(1)证明:因为E为AC的中点,且AC=2BE,所以AE=BE=CE1分所以∠BAE=∠ABE,∠BCE=∠CBE,所以∠BAE+∠BCE=∠ABE+∠CBE=∠ABC2分因为∠BAE+∠BCE+∠ABC=180°,所以∠ABC=90°,即AB⊥BC因为PA⊥平面ABC,且BCC平面ABC,所以PA⊥BC分因为PAC平面PAB,ABC平面PAB,且PA∩AB=A,所以BC⊥平面PAB.5分(2)解:由(1)可知AB,BC·PA两两垂直,则可以以B为原点,BC,BA的方向分别为x,y轴的正方向,过点B作平行于PA的直线为z轴,建立如图所示的空间直角坐标系B-xyz设PA=2,则B(0,0,0),E(3,1,0),P(0,2,2),故BE=(3,1,0),BF=(0,2,2)6分设平面PBE的法向量n=(x,y,z)=3x不妨设x=1,则n=(1,-3,3nb=2y+2=0因为BC⊥平面PAB,所以平面PAB的一个法向量为m=(1,0,0分所以cos(m,n=mm=一…11分设二面角A-PB-E为0,由图可知0为锐角,则cos=7.…12分评分细则:(1)在第一问中,直接由AC=2BE,得到AB⊥BC,没有中间过程,扣2分;(2)在第二问中,可以用传统做法,取AB的中点M,PB的四等分点N(靠近点B),连接MN,ME,EN(图略),则二面角A-PB-E为∠MNE结合题中等量关系,由余弦定理求出cos∠MNE,即得出二面角APB-E的余弦值,只要计算正确,不予扣分,若空间坐标系建立不同,只要建系正确,计算正确,不予扣分;(3)若用其他解法,参照评分标准按步给分

B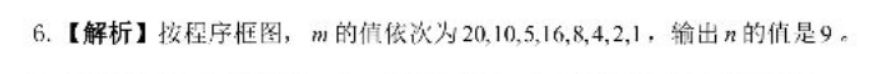

6.【解析】按程序框图,m的值依次为20.10.5,16,8,4,2,1,输出n的值是9。