2022届智慧上进·限时特训·40分钟·分科模拟卷(二)2理科数学答案

2022届智慧上进·限时特训·40分钟·分科模拟卷(二)2理科数学答案，目前我们已经整理了2022届智慧上进·限时特训·40分钟·分科模拟卷(二)2理科数学答案的各科答案和试卷，更多试卷答案请关注本答案网。

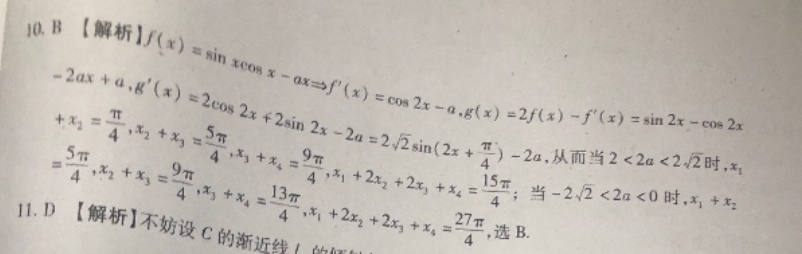
10 B (NAR\J(x) a sin cos x-axsf'(x)=cos 2x-a,8(x)=2/(x)-/'(x)=sin 2r-cos2x-2ax+a,g(x)=2082x+2sin2x-2a=22in(2x+4)-2a,从而当2<2a<22时,x+为4=544,31+2x4+x=32+2x2+x411解析】不妨设C的渐近件当-220时4,x1+2xtx.27T选B.4

2.解:(1)设P(x,y),D(xny0),则A(x0,0),B(0,y),由题意知|AB=1,所以PA=2AB,得(x0-x,-y)=2(-x0,y0),所以y因为x2+y02=1,得+=1(2)(i)当MN斜率存在时,设MN与圆O的切线为y=kx+n,要使四边形OMQN的面积最大,则Q到MN距离要最大,此时过Q点MN的平行线必与椭圆C相切,设为y=kx+m,易得Q到MN距离与O到MN距离之和等于O到直线y=kx+m的距离,设O到直线y=kx+m的距离记为d,则d=my=kr+n,联立x+y=1消去y得(9k2+4)x2+18x+9(m2-4)=0设M(x1,y),N(x2,y2),x+x2=18kn9k2+49k2+412√1+k2√9k2+4-n所以MNF=Ⅵ1+k2|x-x29k2+4因为y=kx+n与圆O相切,所以1+k因为y=kx+m与椭圆相切,(r+m)=1,(4+9k2)x2+18kmx+9m2-36=0,由△=0得9k2+4=m2,1、121+k2×y92+4-n2.|mS=边形O=SamN+Sao=2MN|×d9k2+4k9k2+49k2+44可得S边形OMw随k的增大而增大,即S边形Oo<42(i)当MN斜率不存在时,不妨取MV√23),此时Q(3,0),4√综上所得四边形OMQN的面积的最大值为4