2020年八省联考数学试卷及答案

2020年八省联考数学试卷及答案 ，目前我们已经整理了2020年八省联考数学试卷及答案 的各科答案和试卷，更多试卷答案请关注本答案网。

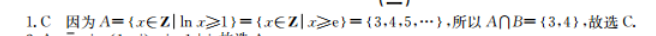
1.C因为A={x∈Z|lnx≥1}={x∈Zlx≥e}={3,4,5…},所以A∩B={3,4},故选C.

22.解:(1)f(x)当≤0时,f(x)>0f(x)在(0,+∞)上单调递增,无极值;当心>0时,x∈(0,1),f(x)>0,f(x)在(0),上单调递增,x∈(1,+∞),f(x)<0,f(x)在,+∞)上单调递减,函数有极大值()=-ha-1,无极小值(2)由(1)可知当a≤0时,f(x)在(0,+∞)上单调增,不可能有两个零点;当心>0时,函数有极大值f()=-ha-1,令g(x)=x-hx-1(x>0),g(x)=g(x)<0,g(x)在(0,1)上单调递减;x∈(1,+∞),g'(x)>0,g(x)在(1,+∞)上单调递增,函数g(x)有最小值g(1)=0.要使若函数f(x)有两个零点时,必须满足a>0且a≠1下面证明a>0且a≠1时,函数有两个零点因为f(1)=0,所以下面证明f(x)还有另一个零点①当0<<1时,八()=0-ha-1>0,()=2ma+--二+二一加,令h(a)=2alna-a2+1(0 (1)=0,则f() <所以f)在()上有零点,又f)在(,+∞)上单调递减,所以f)在()上有惟一零点,从而f(x)有两个零点②当心> 1时,(4)=-ha-1>0,()=-4×+a=×<0,易证c>可得<4,所以f在(.)上有零点,又f()在(,+∞)上单调递减,所以f()在(,)上有惟一零点,从而f(x)有两个零点综上,a的范围是(01)U(1.+∞)(3)证明:f(x1)-f(x2)=lnn-lnx2+a(n-x)-A(n)-((n2Inn-Inntarzn2Inn-Inn又f(x)2(n-x2)_丑q、4+不妨设0 1),则OD=-+b)2<0因此h(1)在(1,+∞)上单调递减,所以h(t) 0.所以f(n+)-k<0.即f(m2)<12分