2022届普通高校招生考试冲刺压轴卷(一)1文科数学N答案

2022届普通高校招生考试冲刺压轴卷(一)1文科数学N答案，目前我们已经整理了2022届普通高校招生考试冲刺压轴卷(一)1文科数学N答案的各科答案和试卷，更多试卷答案请关注本答案网。

0,解得a=√1319.(1)证明:取AD中点0,连接OP,OBM(12分)因为底面四边形ABCD为菱形,∠BAD=60°,所以AD=AB=BD因为O为AD的中点,所以OB⊥AD.(1分)因为△PAD为等腰直角三角形,∠APD=90°,所以PO⊥AD.(2分)因为PO∩OB=0,所以AD⊥平面POB.(3分)因为AD∥BC,所以BC⊥平面POB而PBC平面POB,所以BC⊥PB,故△PBC为直角三角形.(5分)(2)解:因为四边形ABCD是边长为2的菱形,所以PO=1,OB=3又PB=2,所以PO2+0B2=PB2,所以PO⊥OB所以OA,OB,OP所在的直线两两互相垂直以O为坐标原点,分别以OA,OB,OP所在直线为x轴,y轴,轴建立如图所示的空间直角坐标系.(6分)由题中数据可得A(1,0,0),B(0,3,0),D(-1,0.0),P(0,0,1),(7分)所以=(10,-1),P=(0,3,-1),B=A6=(-2,0,0).(8分)设平面PAB的法向量为=(x,y,2),m·PA=x-z=0令y=1,得m=(3,1,3).(9分)PB= 3y-z=0设平面PBC的法向量为n=(x2,y,z2),则1,==2=0令y=1,得n=(0,1,3):(10分)Cassiem√7所以cos(m,n)=mm万×27(1分)设二面角A-PB-C为6,由图可知0为钝角,所以c0s0=2所以二面角A-PB-C的余弦值为(12分)71+035+0.20+0.05)×1=1,解得a=0.18,(1分),求出

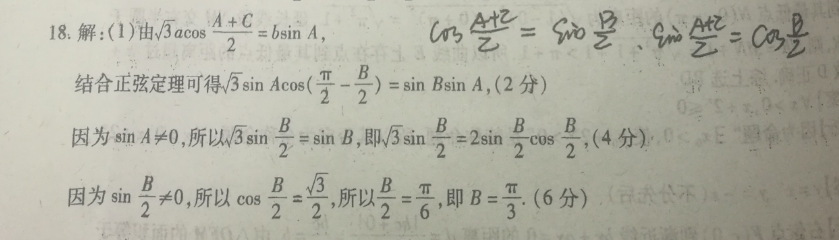
结合正弦定理可得sA(.1.m3t18.解:(1):504+C=b6inA502.9受=C∞22-2)= sin Bsin A,(2分)因为iA≠0,所以smB=mB,即sinB=2mBmB,(4分)因为siB≠0,所以c0s2=2,所以26·即B=m以f与)=(2)在△ABD,△BCD中,分别由余弦定理可得12+(bcos∠ADB=2x/、co∠BDC=-2)2,、(8分所以一12)22×b乙一,整理可得b2=2a2-2,(9分)又在△ABC中,由余弦定理可得B=号2支=,即==+1(0分)联立上述两式得a+a-3=0,解3-1(1)证明:取AD中点O2(12分)