2022届智慧上进·名校学术联盟 高考模拟信息卷 押题卷(十一)11理科数学试题答案

2022届智慧上进·名校学术联盟 高考模拟信息卷 押题卷(十一)11理科数学试题答案，目前我们已经整理了2022届智慧上进·名校学术联盟 高考模拟信息卷 押题卷(十一)11理科数学试题答案的各科答案和试卷，更多试卷答案请关注本答案网。

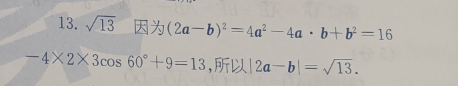
13.√/13因为(2a-b)2=4a2-4a·b+b2=164X2X3cos60°+9=13，所以|2a-b1=√/13.

5.B因为e1,2是表示平面内所有向量的一组基底，所以e,2不共线对于A,若6十=(e-),则11=6无解，所以e十e2与e一e不共线，所以{e十e2,e1-e2}可作为基底对于B,因为-6e,十4e=-2(3e,-2e2),所以30-2e与-6e十4e,共线，所以13e,-2e,-6e十4e2}不可作为基底.1=2k对于C,若e1+2e2=k(e2十2e),则无2=k解，所以e十2e2与e2+2e1不共线，所以{e十2e2,e+2e}可作为基底.对于D,显然，e十e2=e2不可能成立，所以e2与e十e不共线，所以{e2,e1十e2可作为基底.色大上上曰日n为两个亚行的