衢州市2020年6月高二年级教学质量检测试卷语文答案

衢州市2020年6月高二年级教学质量检测试卷语文答案，目前我们已经整理了衢州市2020年6月高二年级教学质量检测试卷语文答案的各科答案和试卷，更多试卷答案请关注本答案网。

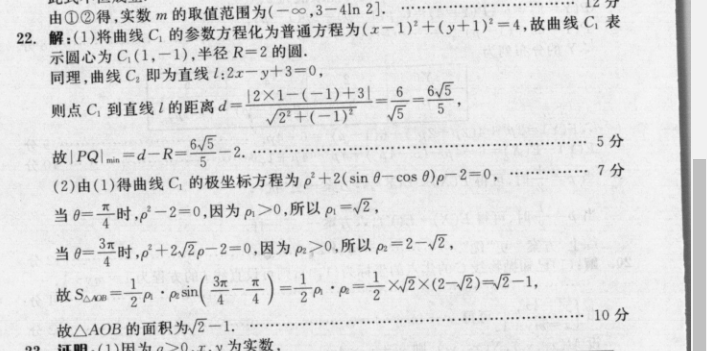
由①②得，实数m的取值范围为（一∞，3一4ln2].22.解：(1)将曲线C1的参数方程化为普通方程为(x一1)2+(y+1)2=4,故曲线C,表示圆心为C(1,一1)，半径R=2的圆.同理，曲线C,即为直线1：2x一y十3=0，则点C到直线1的距离d=12X1-(-1)+3=6=65√/2+(-1)5故1PQ1n=d-R652.5分(2)由(1)得曲线C1的极坐标方程为p2+2(sin0-cos0)p2=0,…7分当0=时，p-2=0,因为Am>0,所以pm=√2，当0=3时，p+2Ep-2=0,因为m>0,所以A=2-√2，故Sw=7A'am(经-）=A'a=号×EX2-E)-E-1,10分故△AOB的面积为2一1./1用为a0..v为实数

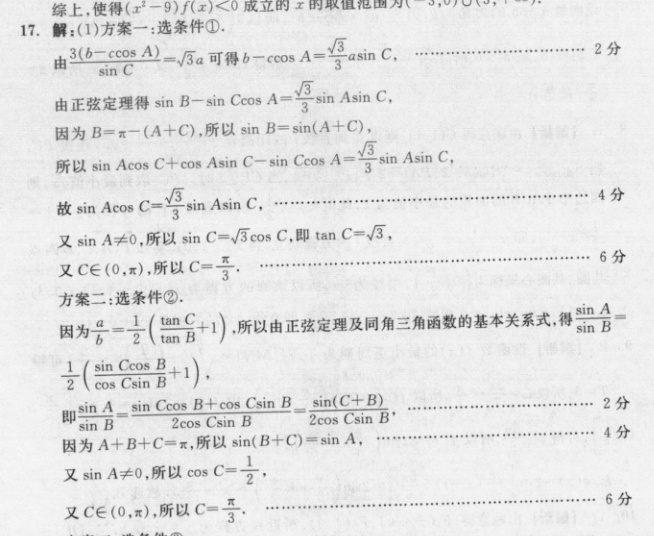
综上，使得(x一9)f(x)<0成立的x的取值把围为(17.解：(1)方案一：选条件①.由36-CA-3a可得6-ce0sA=3asin C.……2分sin C由正弦定理得sinB-sin Ccos A=B3sin Asin C.因为B=r-(A+C),所以sinB=sin(A+C),所以sin Acos C+cos Asin C-sin Ceos A-3 sin Asin C,故n Ac C=9 ninC,4分又sinA≠0，所以sinC=√5cosC,即tanC=√3，又C∈(0，x),所以C=6分方案二：选条件②.因为号一（儡合1），所以由正弦定理及同角三角函数的基本关系式，得出Asin B(+小sin Asin Ccos B+cos Csin Bsin(C+B)………2分sin B2cos Csin B2cos Csin B'因为A+B十C=π，所以sin(B+C)=sinA,4分又nA≠0，所以cosC=又C∈(0，x),所以C=子……6分方案三：选条件③在△ABC中，由正弦定理得bsin C=csin B,……2分因为csin B=6co(c-吾），所以sinC=cos(C-吾），所以mC=cos(c-吾）-号cosC+之nC,所以sinC=√3cosC,即tanC=3,……5分又C∈(0，π)，所以C=子…6分(2②)由题意知5.c一号bnC-号bx号-10厅，可得ab-=40.…8分在△BCD中，由余弦定理得BD-d+号-absC=d+兰-号b>2a·合-2ab-2b-20,当且仅当a=号b,即a=25,b-45时取等号，所以BD的最小值为25.……12分