高考必刷卷2022届普通高等学校招生全国统一考试押题卷(新高考)(一)1数学答案

高考必刷卷2022届普通高等学校招生全国统一考试押题卷(新高考)(一)1数学答案，目前我们已经整理了高考必刷卷2022届普通高等学校招生全国统一考试押题卷(新高考)(一)1数学答案的各科答案和试卷，更多试卷答案请关注本答案网。

20.【命题意图】本题考查利用导数研函数的性质【解析】(1)因为戊22ax-4anx,所以x∈(0,+x)所以(x)=2+2ax24a22(x-a)(x+2a)(2分)①当a>0时,由f(x)>0得x>a;由f(x)<0得0 0得x>-2a;由(x)<0得0 0时、f(x)在(0,a)上单调递减,在(a,+∞)上单调递增②当a<0时、f(x)在(0,-2a)上单调递减,在(-2a,+∞)上单调递增(5分(Ⅱ)若a=0,不等式转化为当x≥1时,xlnx-m(x2-1)≤0恒成立令F(x)=xlnx-m(x2-1),则F'(x)=lnx+1-2mx令(x)=hmx+1-2mx,则G(x)=1-2n更多试题,关注新浪微博《高考倒计时微博》.(6分)①当m≤0时,对任意x∈[1,+∞),恒有F(x)=lnx+1-2mx>0所以F(x)在[1,+∞)上单调递增,所以F(x)≥F(1)=0,所以m≤0不合题意②当m≥时,因为x≥1,所以≤1,所以一-2m≤0,即G'(x)≤0所以6x)在(1,+2)上单调递减,所以Gx)≤()=1-2m≤时=0所以F(x)在[1,+∞)上单调递减,所以F(x)≤F(1)所以m≥符合题意(9分③当0 0,即F'(x)>0,所以F(x上单调递增,所以当x∈1,时,F(x)≥F(1)=0,故0

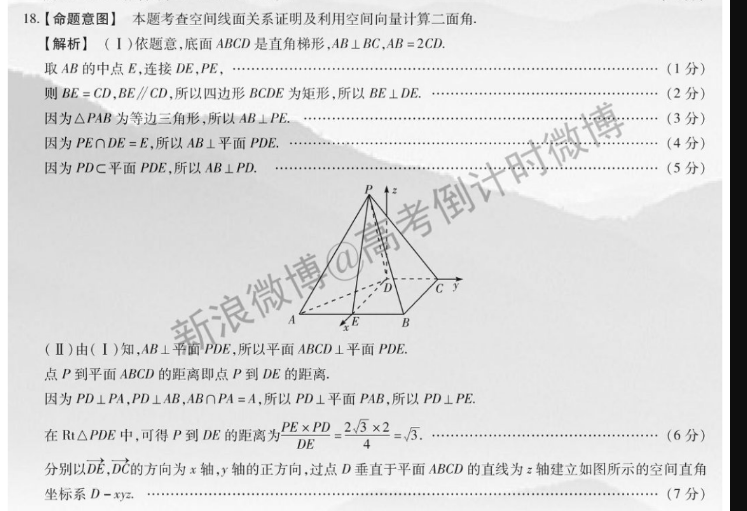
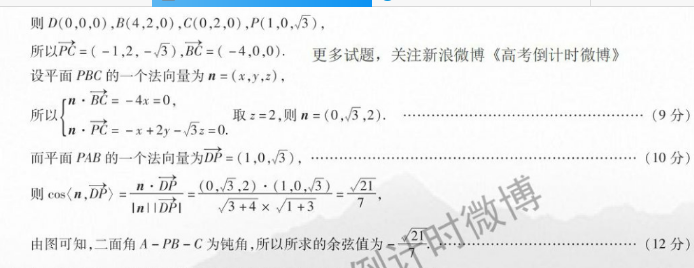
8.【命题意图】本题考查空间线面关系证明及利用空间向量计算二面【解析】(1)依题意,底面ABCD是直角梯形,AB⊥BC,AB=2CD取AB的中点E,连接DE,PE(1分)则BE=CD,BE∥CD,所以四边形BCDE为矩形,所以BE⊥DE(2分)因为△PAB为等边三角形,所以AB⊥PE(3分)因为PE∩DE=E,所以AB⊥平面PDE倒计时微排(4分)因为PDc平面PDE,所以AB⊥PD(5分)(Ⅱ)由(1)知,AB⊥平面PDE,所以平面ABCD⊥平面PDE点P到平面ABCD的距离即点P到DE的距离因为PD⊥PA,PD⊥AB,AB∩PA=A,所以PD⊥平面PAB,所以PD⊥PE在Rt△PDE中,可得P到DE的距离为2=2×2=5(6分)分别以D,D的方向为x轴,y轴的正方向,过点D垂直于平面ABCD的直线为z轴建立如图所示的空间直角坐标系D(7分)则D(0,0,0),B(4,2,0),C(0,2,0),P(1,0,3)所以P=(-1,2,-3),BC=(-4,0.0),更多试题,关注新浪微博《高考倒计时微博》设平面PBC的一个法向量为n=(x,y,z)取z=2,则n=(0,3,2)而平面PAB的一个法向量为DP=(1,0,3),(10分则cos(n,DP)=D(0,3,2)·(10,32nII DPI3+4×√1+3由图可知,二面角A-PB-C为钝角,所以所求的余弦值为(12分