重庆康德2022年普通高等学校招生全国统一考试高三12月调研测试卷数学试题答案

重庆康德2022年普通高等学校招生全国统一考试高三12月调研测试卷数学试题答案，目前我们趣对答案已经整理了重庆康德2022年普通高等学校招生全国统一考试高三12月调研测试卷数学试题答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

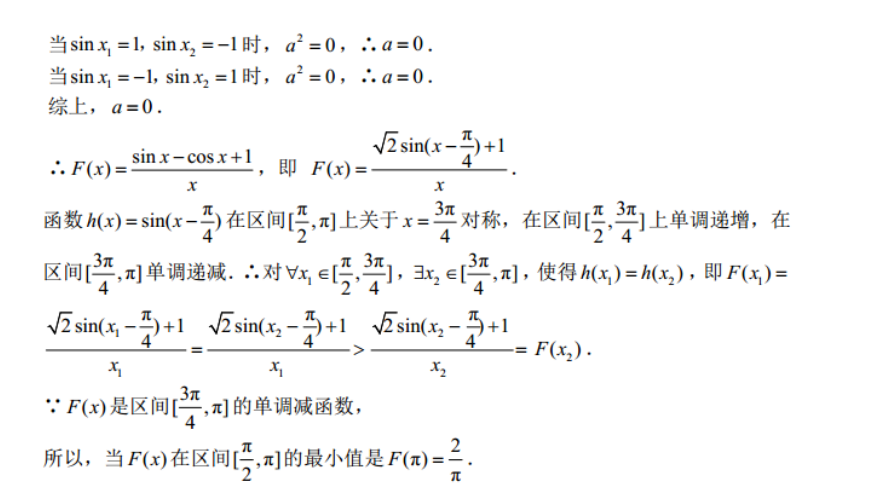
∴ ABAB21.解:(1)∵f(x)=x+a-sinx,f(x)为[O,+∞)上的增函数,∴x≥0,f(x)=x+a-sinx≥0,∴a≥sinx-x设g(x)=sinx-x(x≥0),∵g(x)=cosx-1≤0,∴g(x)为减函数,g(x)≤g(0)=0所以,实数a的取值范围是[0,+∞(2)∵g(x)=f(x)-x2=ax+cosx,∴g'(x)=a-sinx.2设在x,x2处切线相互垂直,∴g'(x1)g'(x2)=-1,ap(a-sin xa-sin x 2)=-1a-(sin x , +sin x 2 )a+sin x, sin x ,+1=0∴Δ=(sinx+sinx2)2-4( Sin x sinr2+1)=(sinx1-sinx2)-4≥0又:(sinx-sinx2)2≤4∴(inx-sinx2)2=4,即sinx1=l,sinx2=-1,或sinx=-1,sinx2=1当six1=L,sinx2=-1时,a2=0,∴a=0当sinx=-l,sinx2=1时,a2=0,∴a=0.综上,a=0.sin x-cosx+I2sin(x--)+1∴F(x),即F(x)函数M(x)=simx-)在区间,上关于x=3对称,在区间,3]上单调递增,在区间[,x]单调递减.对x∈,,丑。3,使得h(x)=h(x2),即F(x)√sin(x-2)+1√sin(x2-2+12sin(x2-2+1∵F(x)是区间[,x的单调减函数,所以,当F(x)在区间[,]的最小值是F(x)=

=—,22.解:(1)消去参数方程中的参数t,得到曲线C的普通方程为y分别将p2=x2+y2,psin=y代入p2(+2sin20)=3即p2+2(psin0)2=3,并化简得曲线C2的直角坐标方程为,∴:4x2-6x=0∴|ABF=√+110-÷设C(√3cos,sin0),点C到AB距离为d,3cosb-sinb-l|√22cos(+-)-122(S)1323√292224不竺