百师联盟·2022届高三信息押题卷(四)4全国卷理科数学答案

百师联盟·2022届高三信息押题卷(四)4全国卷理科数学答案，目前我们已经整理了百师联盟·2022届高三信息押题卷(四)4全国卷理科数学答案的各科答案和试卷，更多试卷答案请关注本答案网。

15.【答案】80【解析】电2cosB=2a+b及正弦定理可得2 2sin C cos B=2sinA+sinB2 e sin C cos B=2sim(B+C)+sinB,即2 sin b cos cut sin B0,又sinB>0,故cosC=-,2故C2,因为△ABC的面积为43,所以 absin c=43,即mb×=43,故2ab=16,由余弦定理可得a2=a2+b2-2 2ab cos c=a2+b2-2×16x(-)=a2+b)16,所以3a2+c2=3a2+a2+b2+16=4a2+b2+16≥4ab+16=80,当且仅当2ab=42时等号成立,故3a2+c2的最小值为80.故答案为:80.

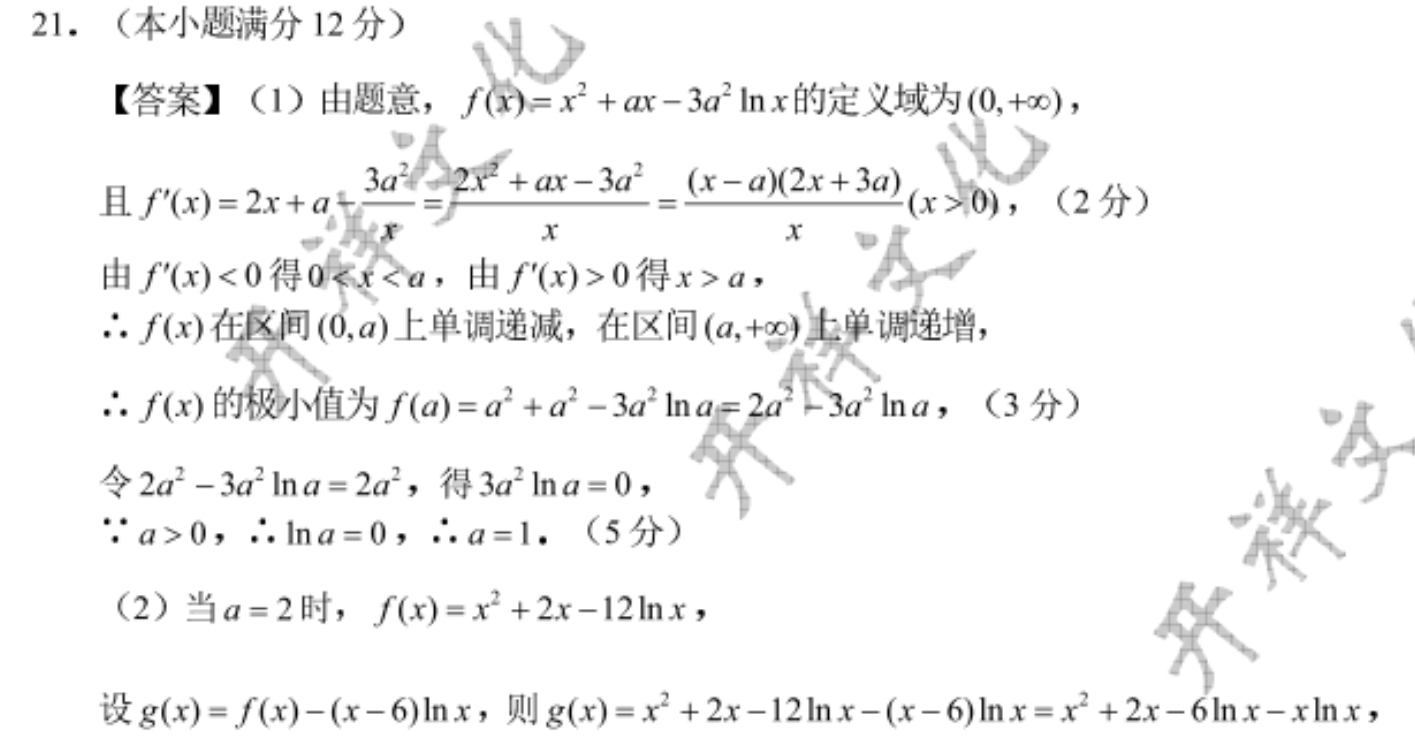
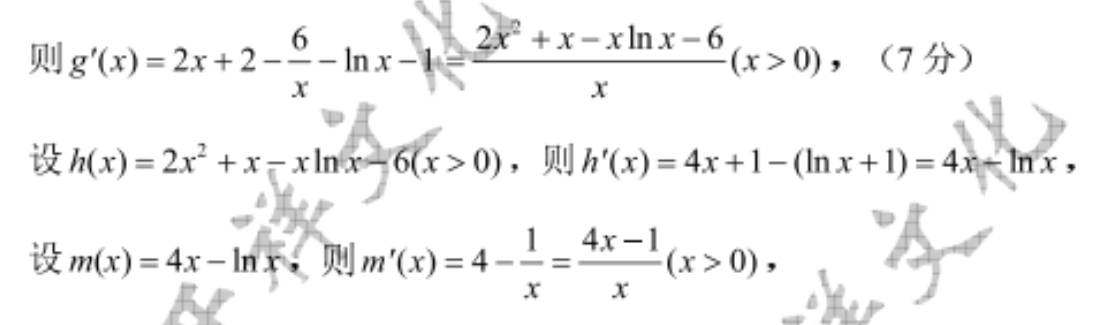
21.(本小题满分12分)【答案】(1)由题意,f(x)=x2+ax-3a2hx的定义域为(,+∞),且f(x)=2x+a3a2=2x2+ax-3a2(x-a)(2x+3a)(x>0),(2分)x由f(x)<0得0xa,由f(x)>0得x>a,f(x)在区间(0,a)上单调递减,在区间(a,+x)上单调递增,f(x)的极小值为f(a2=a2+a2-32lma=2413ma,(3分)令2a2-3a2lna=2a2,得3a2lna=0>0,01.(5分)(2)当a=2时,f(x)=x2+2x-12hnx,it g(x)=f(x)-(x-6)Inx, g(x)=x+2x-12In x-(x-6)Inx=x+2x-6Inx-xInx,则g(x)=2x+2、6+x-xInx-6Inx-1e(x>0),(7分)ih(x)=2x2+x-xlnx-6(x>0), A'(x)=4x+1-(Inx+1)=4x-Inx设m)=4x-hm不则m()=4-1=4x-1(x>0),由m(x)<0可得0 0可得x>,即m(x)在(0,-)上单调递减,在(-,+∞)上单调递增,∴m(x)≥m()=1-ln=1+2ln2>0,即h(x)>0,4h(x)在(0,+∞)上单调递增。(9分)∵h()=-3<0,(2)=4-2n2>0,∴M(x)存在唯的零点x,且x∈(1,2)由h(x)=2x2+x。- x In x0-6=0,得hnx=2x--+1,当x∈(0,x)时,M(x)<0,即g'(x)<0,当x∈(x,+∞)时,h(x)>0,即g(x)>0,8(x)2g(x0)=x2+2x0-6hx-xmx=x+2x-(6+x2~6+1)36x2-11x+36易得g(x)在区间(1,2)上单调递减,故g(x)>-2-1192-8,g(x)=f(x)+(x6)hnx>-8,即f(x)>(x-6)hx8.4(12分)(解法三当a=2时,f(x)=x2+2x-12lnx要证f(x)>(x-6)hnx-8,只要证x2+2x-12lnx>(x-6)lnx-8,即证x2+2x+8>(x+6)hnx,∴x>0,∴只要证x2+2x+8x+6>lnx,(7分)下面证明x2+2x+8xx+6>①,H>lnx②,2x2-2x+16=(x-12+15≥15>0,2x2+4x+16%6x,结合x>0,得+2x+8x+6即当x>0时,①成立;(9分)令M(x)=-lnx,则h(x)=22 x 2x当0 2时,h(x)>0,∴函数h(x)在(0,2)上单调递减,在(2,+∞)上单调递增,函数h(x)的最小值为h2)2n2=1-hm2,又1-ln2>1-lne=0,h(x)>0∴②成立综合①②可知x2+2x+8x>->Inx,x+6∴f(x)>(x-6)lnx-8成立,(12分)