2022年普通高等学校招生全国统一考试(老高考)T8联盟·压轴卷(二)2文科综合试题答案

2022年普通高等学校招生全国统一考试(老高考)T8联盟·压轴卷(二)2文科综合试题答案，目前我们已经整理了2022年普通高等学校招生全国统一考试(老高考)T8联盟·压轴卷(二)2文科综合试题答案的各科答案和试卷，更多试卷答案请关注本答案网。

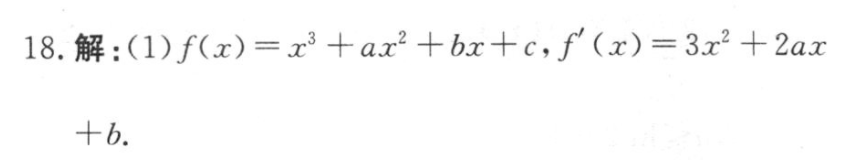
18.解：(1)f(x)=x3+ax2+bx+c,f(x)=3x2+2ax+b.f(-号)-号-音a+b=0a=-由解得f(1)=3+2a+b=0,b=-2.(2分)f(x)=3x2-x-2=(3x+2)(x-1),函数f(x),f(x)的变化情况如下表：1(1,十oo(x00极大值极小值所以函数f(x)的单调递增区间是（一©，一号）和(1,十∞)，单调递减区间是(-号，1)(5分)(2)因为fx)=r-2r-2x+cxe[-1,2],根据(1)得f(x)在(-1，-号)上单调递增，在号，1)上单调递减，在1,2)上单调递增，所以当x=一时，f(x)-器+c为极大值，而f2)-2+c>器+e,所以2)=2+c为最大值。(9分)要使f(x) f(2)=2+c.解得c<1或c>2.(12分)

20.解：(1)因为f(x)=xnx,所以f(x)=lnx+1,令f(x)=0,得x=是，因为当x∈(0，。)时，了(x)<0:当x∈(日，+∞)时，f(x)>0.所以函数∫(x)在(0，。]上单调递减，在[日，+∞)上单调递增。(4分)(2)由题可得不等式(a+1)nx+-ax+a-1<0在(1，十oo)上恒成立，(5分)设h(x)=(a+1)lnx+-ar十a-1,则h'(x)=--a=-(ar-.(6分)①当a≤0时，因为h'(x)>0在(1，+∞)上恒成立，所以h(x)在(1，十∞)上是增函数，又因为h(1)=0,所以当x∈(1，+o∞)时，总有h(x)>0,不符合题意.(8分)②当a≥1时，因为'(x)<0在(1，+∞)上恒成立，所以h(x)在(1，十∞)上是减函数，又因为h(1)=0,所以当x∈(1，十∞)时，总有h(x)<0,符合题意.(10分)⊙当0 0,不符合题意.综上，实数a的取值范围为[1，十o∞).(12分)