2022年全国高考·调研模拟卷G-Y(一)1文科数学答案

2022年全国高考·调研模拟卷G-Y(一)1文科数学答案，目前我们趣对答案已经整理了2022年全国高考·调研模拟卷G-Y(一)1文科数学答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

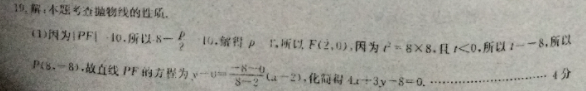
解:本题考查抛物线的性为P0所以8一5B缩p以F(20),两为88,且C所以:一8所以8,8),故直线PF的方程为y(x-2),化4x+3y-8=0.(3(a)线C的方程为y一,联立方Vy+6y-16=0设直线m的力程为y+8-k(x-8),联立bH·by2一8“-6-0,由△=0,解k一}所以直线=的方程为x+2中8一,同理可得直线的方程为2-y+1=,由{+2)一。解得2x=y+1=即G-2.-3),设点G(-2,-3)直线PQ的距离为,=3D,所以△的积为号××号早12分【解题思路】解决直线与抛物线的综合问题时,需要注意(1)观察、应用题没中的每一个条件,明确确定直线、抛物线的条什(2)强化有关直线与抛物线得出一元二次方程后的运算能力,重视根与系数之间的关系,弦长,斜率,三角形的面积等问题;(3)注至平面几何的知识,利用数形结合的思想处理问

19.证明:(1)如图,作PO⊥CD于点O,连接OA,则点O是CD的中点因为底面ABCD是面积为23的菱形,所以 1DXDCX sin∠ADC=23,即2×2Xsn∠ADC=2/32分D由∠ADC为锐角,得∠ADC=60又因为DO=1,AD=2OM1,PC平面PAO.CA∩PA=1所以CD⊥平面PA因为PAC平面PA0,所以CD⊥PA取P4的中点N,连接ON,M/N因为点M为PB的中点,所以n证MN∠(X所以四边形MNX为平行四边形.所以CM∥ON在△PYA中,OP=(A14=3,N为PA中点所以ON⊥PA,所以CM⊥PA又因为(M,CDC平面CDM,CM∩CD=C所以PA⊥平面CDM因为DMC平面CDM.所以PA⊥DM解:(2)因为侧面PDC⊥底面ABCD所以点B到平面PDC的距离为 BCsin60=2x3因为M为PB的中点,所以点M到平面PDC的距离为所以V能二35m,1××2X2x×23=1