2022届百校联盟高三12月考试(福建)英语答案

2022届百校联盟高三12月考试(福建)英语答案，目前我们趣对答案已经整理了2022届百校联盟高三12月考试(福建)英语答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

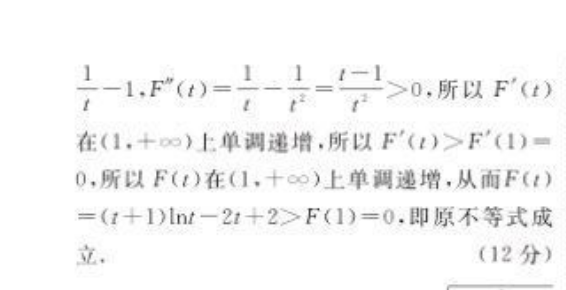
21解:(I)由题意得f'(x)≤0在(0,+∞)上恒成立(1分)因为f(x)=2xlnx+x-ax2-3x=x(2lnrax-2),所以2lnx-ax-2≤0在(0,+∞)上clue恒成立,即一≤a在(0,+∞)上恒成立(3分)令g(x)2lnx-2,则g'(x)=2(2-lnx)x∈(0,e2)时,g'(x)>0,比时g(x)单调递增;当x∈(e2,+∞)时,g'(x)<0,此时g(x)单调遊减所以当x=e2时,函数g(x)有极大值,也是最大值所以a≥g(e2)=2故实数a的取值范围为[一,+(5分)(Ⅱ)证明:由:I)知f(x)=x(2lnx-ax2),则2inxi=ax1+22nx2=ax2+2所以2lnx1x2=a(x1+x2)+4,2ln==a(x12In可得21nx、x2r1-x2(x1+r2)+4.(7分因为x1≠x2…,不妨设x1>x`2,则1nx、x2Int+2(8分)令h(t)=—nt+2,t>1.要证h(t)+2>4在(1,+∞)上恒成立,即证(x+1)ln2t+2>0.(9分)令F(t)=(t+1)nt-2t+2,则F'(t)=lnt+1,F(t)=-=x>0,所以F()在(1,+∞)上单调递增,所以F'()>F'(1)=0,所以F(t)在(1,+∞)上单调递增,从而F(t)(+1)lnt-21+2>F(1)=0,即原不等式成(12分)

【语篇导读】本文是新闻报道。在新冠肺炎流行期间,很多居家的人们想起了为了躲避纳粹迫害而到处躲藏的安妮·弗兰克,安妮在日记中表现出的坚强引导人们如何去正确看待居家躲避病毒。28.B【解析】细节理解题。根据第二段中的 The anneFrank Project . is working to feed and fund students inneed可知,安妮·弗兰克项目旨在帮助有困难的学生,为他们提供食物和资金。故选B。29.A【解析】推理判断题。根据第二段中的 Whileare not hiding from the Nazis, we are indeed hidingrom an oppressiveⅵinus.可知,人们在新冠肺炎爆发而居家期间想到安妮是因为他们都要躲着不能外出,一个是躲避纳粹,个是躲避病毒。故选A30C【解析】推理判断题。根据第三段中的whatAnne has offered for decades is an example of npt justtragedy(悲剧), but also strength, kindness and, grace可知,Gsar认为安妮在躲避纳粹期间表现得非常坚强。故选C。31.D,【解析】细节理解题。根据第四段内容可知,Ruth franklin建议人们在与疫情斗争的困难时期记录下自己生活的点滴。故选D。