衡水金卷先享题 2022-2023学年度上学期高三年级一调考试(湖南专版)物理答案

衡水金卷先享题 2022-2023学年度上学期高三年级一调考试(湖南专版)物理答案，目前我们已经整理了衡水金卷先享题 2022-2023学年度上学期高三年级一调考试(湖南专版)物理答案的各科答案和试卷，更多试卷答案请关注本答案网。

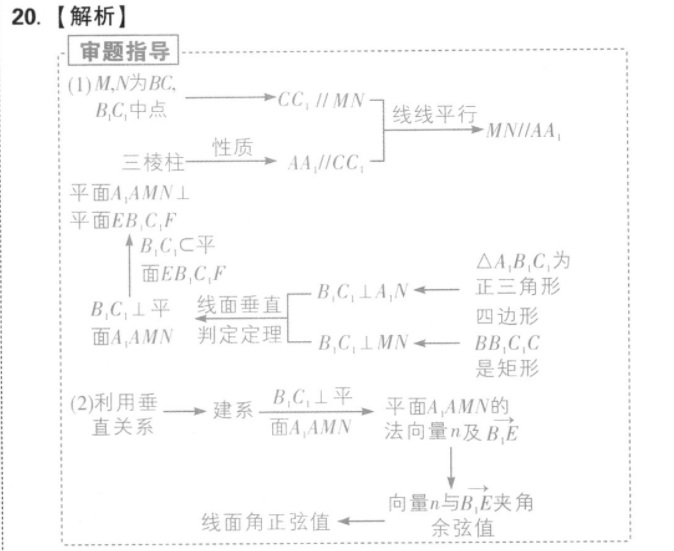
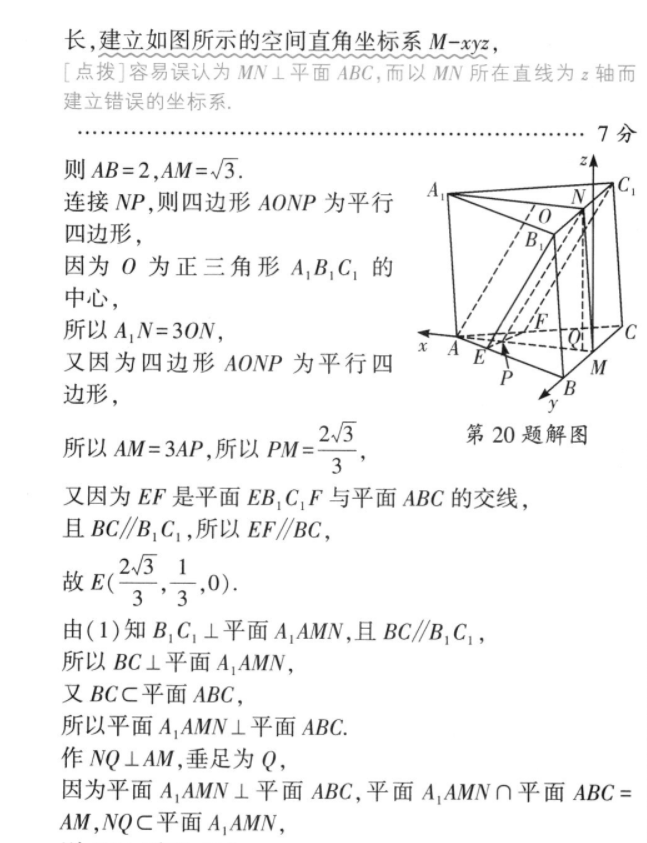
20.【解析】审题指导I)M,N为BCB,C中点-CC.//MN线线平行MNIIAA性质三棱柱平面A,AMN⊥平面EBC,FB,CC平面EB,CF△A,B,C,为线面垂直BC⊥A,N—正三角形B,C,⊥平四边形面A.AMN判定定理B,C,⊥MN←BB.C C是矩形2)利用垂建系B,C,⊥平平面A,AMN的直关系面AAMN法向量n及B,E向量n与B,E夹角线面角正弦值←一余弦值解：(1)因为M,N分别为BC,B,C,的中点，所以MN∥CC1[点拨]利用平行四边形和中位线性质证明线线平行又由三棱柱的性质得AA,∥CC,故AA,∥MN.…2分因为△AB,C,是正三角形，N为B,C1的中点，所以B,C,⊥A,N又B,C,⊥MN,A,N∩MW=N,故B,C1⊥平面A,AMW.4分又B,C,C平面EB,C,F,所以平面A,AMN⊥平面EB,C,F.6分(2)由△ABC为等边三角形及M为BC中点得AML⊥BC.以M为坐标原点，MA的方向为x轴正方向，1MB1为单位长，建立如图所示的空间直角坐标系M-xyz,[点拨]容易误认为MW⊥平面ABC,而以MN所在直线为z轴而建立错误的坐标系，则AB=2,AM=√5.连接NP,则四边形AONP为平行四边形.因为0为正三角形A,B,C,的中心，所以A,N=3ON,又因为四边形AONP为平行四边形，23所以AM=3AP,所以PM=第20题解图3又因为EF是平面EB,C,F与平面ABC的交线，且BC∥B,C,所以EF∥BC,故33,02w31由(1)知B,C,⊥平面A,AMN,且BC∥B,C1,所以BC⊥平面A,AMN,又BCC平面ABC所以平面A,AMN⊥平面ABC.作NQ⊥AM,垂足为Q,因为平面A,AMN⊥平面ABC,平面A,AMN∩平面ABC=AM,NQC平面A,AMN,则NQ⊥平面ABC23设Q(a,0,0),则PQ=3-a,由四边形A0NP为平行四边形得AO=NP=AB=2,则Q=vP-P0√4-(2。(a.a))........................9分故正-(25，子4-(29，B=23又n=(0,-1,0)是平面A,AMN的一个法向量，n·B,E故sin(7-(n,B应或)=cos(m,B》=-1010nl·IB,E1[点拨]将线面角的正弦值转化为直线的方向向量与平面法向量夹角的余弦值，得到直线B,E与平面A,AMN所成角的正弦值11分所以直线B,E与平面A,AMN所成角的正弦值为/101012分

4.C【考查点】本题考查数列在数学文化中的应用信息提取1]最上层第一环有9块扇面形石板「2]每环比上一环多9块，下一层的第一环比上一层的最后环多9块：[3]每层环数相同，且下层比中层多729块【解析】已知最上层第一环是9块扇面形石板，设每层有n环，从上至下，3层共计3n环，因为扇面形石板向外每环依次增加9块，且下一层的第一环比上一层的最后一环多9块，所以这3n环扇面形石板块数构成等差数列{a所以a,=9,公差d=9,[点拨]根据相邻两环之间扇面形石板块数之间的关系，将实际问题转化为等差数列，进而得出首项和公差记三层的扇面形石板块数分别为Sn,S2n-S,Sn-S,由等差数列性质可知Sn,S2n-Sn,Sn-S2n成等差数列，且公差为729，因为S=a27d8=2a,2n2-》,2S=3nm,+3n（30-D4,2故(S3n-S2n）-(S2n-Sn)=n2d=729,因为n>0,27×(9+9+26×9）所以n=9,所以3n=27,S2,==3402.2故三层共有扇面形石板3402块，