2023届金太阳重庆高三9月联考(802C·C QING)地理答案

2023届金太阳重庆高三9月联考(802C·C QING)地理答案，目前我们已经整理了2023届金太阳重庆高三9月联考(802C·C QING)地理答案的各科答案和试卷，更多试卷答案请关注本答案网。

19.(12分)如图，已如椭图C亏+号-1与直线1：后+言-1，点P在直线1上，由点P引椭圆C的两条切线PA,PBA,B为切点，O是坐标原点，(1)若P为直线l与y轴的交点，求△PAB的面积S;(2)若OD⊥AB,D为垂足，证明：存在定点Q,使得|DQ|为定值.(1)解：由题意知P(0,3),过点P与椭圆相切的直线斜率存在，设切线方程为y=kx十3，联立P=x+3,x2+2y2=6,可得(2k2+1)x2+12kx+12=0(*),由△=144k2-48(2k2+1)=48(k2-1)=0,可得k=士1，即切线方程为y=士x十3，所以PA⊥PB.将k=1代入方程(*)可得x2+4x十4=0，解得x=一2，此时y=1,不妨设A(-2,1),同理可得B(2,1),|PA|=|PB|=√4+(1-3)=2√2，因此，SAPAB=PA·IPB1=2)证明：先证明椭圆号+号=1在其上一点M(x0o)处的切线方程为乙0+631.因为点M(xy)在椭国号十3=1上，所以z号+2y=6=1,63联立x21y2消去y可得6十3x-9+1-36306+3=1,整理得x2一2x0x十x6=0,即(x一x0)2=0,解得x=x0,=1.因此，精国5+=1在其上一点M(xy,)处的切线方程为g+写63受A,B则初线PA的方程为号+号-1，物我PB的方程为晋+3=1.04mx+n1=1,6设P(m,n),则mx2+ny2=1,63所以点A,B的坐标满足方程mx十2ny一6=0，所以直线AB的方程为mx十2ny一6=0.山旺心容不站：m坐随克出，0因为点P(mm)在直线后+学-1上，则m十2m=6,则2m=6-m,所以直线AB的方程可表示为mx十(6一m)y一6=0，即m(x一y)十6(y一1)=0，白8可得仁燕直我AB进定点T1山.y=1,因为OD⊥AB,所以，点D在以OT为直径的圆上，当Q为线段OT的中点时，DQ1=10T-受，此时点Q的全标为（公，号》故存在点Q(分，》，使得1DQ1为定值号

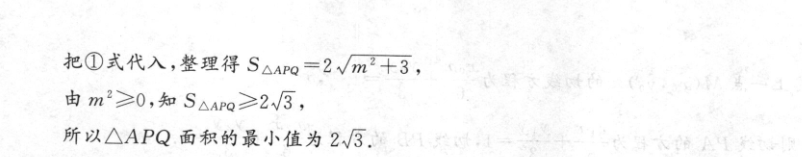
20.(12分)设圆E后+兰-1a6>0经过点M3,号》，离心率为号22(1)求椭圆E的标准方程；(2)设椭圆E的右顶点为A,过定点N(1,0)且斜率不为0的直线与椭圆E交于B,C两点，设直线AB,AC与直线x=4的交点分别为P,Q,求△APQ面积的最小值.层+62=1,a=2,解：(1)由题意知，e=3解得b=1,a 2'c=√3，a2=b2+c2,所以精围E的标准方程为号十y=1。(2)设过点N(1,0)且斜率不为0的直线方程为x=my十1，代入椭圆E的方程，整理得(m2十4)y2十2my一3=0，△=4m2+12(m2+4)=16(m2+3)>0,-2m3设B(x1),C(x).则y+y-m千4y=m2+4①，由(1)得A(2,0),个平交时则直线AB的方程为y=y（z-2),流A:立0，气点平信议交众平证阳M,克州一x1-2西阳。避爽水令x=4,得yP=2y1。,同理可得y0=x2一22y2x1一2则S△APO=12X(4-2)·lPQ=|PQ1=|yp-yo1=2y12y2-2x4-2/,)林坐站1M支好(【·将x1=my1+1,x2=my2十1代入，2y12y2=2×y1-y2W/(y1+y2)2-4y1y2可得S△APQ=my1-1my2-1m2y1y2-m(y,+y2)+=2×m2y1y2-m(y1+y2)+1把①式代入，整理得S△AP0=2√m十3，由m2≥0，知S△AP阳≥2√3，所以△APQ面积的最小值为2√3.