2022届先知新课标月考卷(四)4文科数学试题答案

2022届先知新课标月考卷(四)4文科数学试题答案，目前我们趣对答案已经整理了2022届先知新课标月考卷(四)4文科数学试题答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

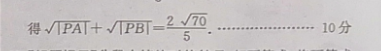
22.【解题提示】(1)将曲线C的参数方程化为曲线C的直repos角坐标方程,代人化为极坐标方程(2)利用参数力程中的参数的几何意义,结合根与系数的关系求解【解析】(1)曲线C的直角坐标力程为x2+(y-2)2=9,即x2+y2=4y+5,2分因为y=psin O,所以=4psin0+5,故曲线C的极坐标方程为p2=4msin0+55分(2)将(为参数)化为(为3参数)代入x2+(y-2)2=9,得2+4=0.设A,B两点对应的参数分别为1,12则367分因为点P的极坐标为(3,x),所以点P的直角坐标为(-3,0),所以(√TPAI+√PB)2=1PA|+|PB|+2√PA·IPB++2v256得PAI+√TPB=2√010分

9.(本小题满分12分)解:(1)性质1:DE⊥平面ABD.证明如下:翻折前,DE⊥D4,DE⊥BC,翻折后仍然有DE⊥D,DE⊥DB,且D∩DB=D则DE⊥平面ABD性质2:DE⊥AB,证明如下:与性质1证明方法相同,得到DE又因ABc平面ABD,则DEMB性质3DE与平面ABD一直线都垂直.证明如下与性质1证明方得到DE⊥平面ABD,从而DE与平面ABD内任一直线都垂直性质4:直线DE与平面ABE所成角等于一.证明如下如图5,取AB的中点F,连接DF,EF由DA=DB,得DF⊥AB,与性质2证明相同,得DE⊥AB,DE⊥DF再因DE∩DF=D,则AB⊥平面DEF,进而平面DEF⊥平面ABE作DH⊥EF于H,则DH⊥平面ABE,∠DEF就是直线DE与采面ABE所成的角DE=l, EF=cos∠DEF、DE22说明:写出一条并且只需写出一条正确的(允许在以上4条之外),给3分,完成正确的证明后合计给5分(2)解法一:AD=BD=√2,AB=2则△ABD是等腰直角三角形,如图6,取AB的中点F,则F是△ABD的外心图6设几何体E-ABD外接球的球心是O,则OF⊥平面ABD作OM⊥DE于M,则M是DE的中点,OFDM是矩形,OF=DMB=1几何体E-ABD的外接球半径R=√OF+FD2=+1=,则外接球的体积v=-R(12分)解法二:证明D,DB,DE两两垂信后,几何体E-ABD外接球就是以D4,DB,DE相邻的棱的长方体的外接球、(√5D4-+DB-+DE=2+2+1=5,R(12分)