衡中同卷 2022-2023学年度上学期高三年级期中考试(全国卷)历史试题答案,目前我们已经整理了衡中同卷 2022-2023学年度上学期高三年级期中考试(全国卷)历史试题答案的各科答案和试卷,更多试卷答案请关注本答案网。

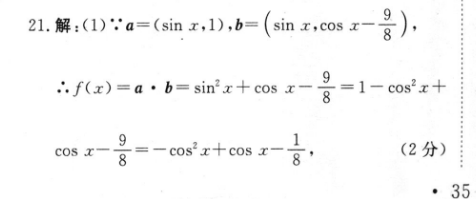


21.解:(1):a=(sinx,l1),b=(sinx,cosx-号)f(x)=a·b=sin2x+cosx-号=1-cos2x+cos x-98(2分)·35∴fx)=-(eosx-2)广+日,,x∈[0,π],.-1≤cosx≤1,-晋
f(x)十h(x)十sin2x在x∈[0,受]上有解,依题意,不等式m>f(x)+h(x)十sin2x在x∈[0,受]上有解,设y-f)+A()十sm2z=cosx-mx-号+2sin xcos x=2 2sin rco+cosx-sinx-号xe[0,登]令t=cosx-sinx=Ecos(x+开),则2 sin xcos=1-t,(8分)ve[o.].t∈[-1,1],则y=-+-}=-(-号)te[-1,1,∴当=-1时y取得最小值-?,(10分)'.m>ymin=-94故实数m的取值范围为(-号,十∞)上(12分)




20.解:(1)由题得,f(x)=2+2ax一4a=2(a2-2ax+1D(x>0),(1分)x令g(x)=a.x2-2a.x+1(x>0),①当a=0时,g(x)=1>0,在(0,+∞)上,f(x)>0,所以f(x)单调递增.(2分)②当a<0时,△=4a2-4a=4a(a-1)>0,令g)=0,得=0-a,=十瓜-aa且x1>0>x2,所以当x∈(0,x1)时,f(x)>0,所以f(x)单调递增;当x∈(x1,+∞)时,f(x)<0,所以f(x)单调递减.(4分)③当a>0时,△=4a(a-1),当0
0,所以f(x)单调递增.当a>1时,△=4a2-4a=4a(a-1)>0,令g)=0,得-a,,=+V-aaa且0
0,所以f(x)单调递增;当x∈(x1,x2)时,f(x)<0,所以f(x)单调递减.综上可得:当a<0时,f(x)在(o,a-)上单调递增,在a,十∞)上单调递减当0≤a≤1时,f(x)在(0,十o∞)上单调递增;当0>1时f()在(,)月aa十aa,十o∞)上单调递减(6分)(2)因为f(1)=0,根据(1)的讨论可知,当0≤a≤1时,f(x)在(0,+∞)上单调递增,所以f(x)在(1,十∞)上单调递增,所以f(x)>f(1)=0成立.(8分)当a<0时,f(x)在(x1,十∞)上单调递减,x→+∞时,f(x)+一o∞,所以存在x∈(x1,十∞)使得f(x)<0,故此时不成立(9分)当a>1时,f(x)在(0,x),(x2,+o∞)上单调递增;在(,)上单调递减,而=-aa<1<_a+va-aa所以当x∈(1,x2)时,f(x)单调递减,此时f(x)