2022年六安市省示范高中高三教学质量检测文科数学答案

2022年六安市省示范高中高三教学质量检测文科数学答案，目前我们趣对答案已经整理了2022年六安市省示范高中高三教学质量检测文科数学答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

17.【试题情境】本题是基础性题目,属于课程学习情境,具体是数学运算学习情境【必备知识】本題考查的知识是“掌握等差数列、等比数到列的通项公式与前n项和公式【关键能力】本题考查逻辑思维能力、运算求解能力【解题思路】(1)a2·a3=a,a3=25设等比数列{a}的公比为q(q>0)b2h。+bn->02(S。-n)(2)由(1)锴位相减法解:(1)设等比数列}an的公比为q(q>0)a2·a3=a1,a=256,∴a1q·a1q=a1q,a1q3=256,(2分)(3分2Sn=b2+b,-2①当n=1时,2S1=2b1=b2+b1-2,解得b1=2或b1=-1(舍去);(4分)当n=1时,2S1=2b1=b2+b1-2,解得b1=2或b1=-1(舍去);(4分)当n≥2时,2Sn1=b21+b,1-2②,①-②得2b,=62-b2+bn-b,即(b+b)(b-b,1-1)=0,b。+b。1>0,b。-b1-1=0,即b。-b-1=1.(5分)∴数列{b,|是以2为首项,1为公差的等差数列,bn=2+(n-1)×1=n+1.(6分)(2)由(1)可得S=m(n+1+2)_n2+3n3n)·2”1C,=M,=1×2+2x23+3×24+…+(n-1)×2"+nx2"“,(9分)2M=1×23+2×2+3×23+…+(n-1)×2+n×22,(10分)故-M,=22+23+24+25+22[4+(n-1)×22],(11分)∴M,=4+(n-1)×2n(12分)解后反思》在解决数列求和问题时,首先需要判断数列通项的特征,然后选择合适的求和方法,如本题中数列{cn}的通项是一个等差数列和一个等比数列的通项的积,故采用错位相减法求数列{cn}的前n项和

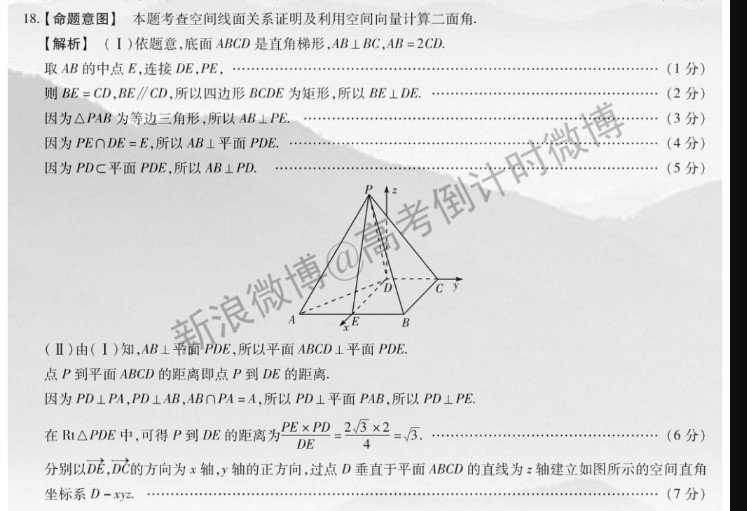
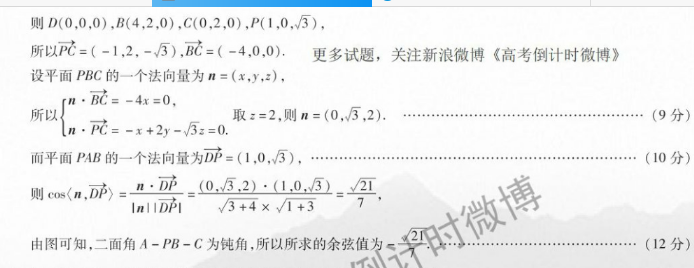
8.【命题意图】本题考查空间线面关系证明及利用空间向量计算二面【解析】(1)依题意,底面ABCD是直角梯形,AB⊥BC,AB=2CD取AB的中点E,连接DE,PE(1分)则BE=CD,BE∥CD,所以四边形BCDE为矩形,所以BE⊥DE(2分)因为△PAB为等边三角形,所以AB⊥PE(3分)因为PE∩DE=E,所以AB⊥平面PDE倒计时微排(4分)因为PDc平面PDE,所以AB⊥PD(5分)(Ⅱ)由(1)知,AB⊥平面PDE,所以平面ABCD⊥平面PDE点P到平面ABCD的距离即点P到DE的距离因为PD⊥PA,PD⊥AB,AB∩PA=A,所以PD⊥平面PAB,所以PD⊥PE在Rt△PDE中,可得P到DE的距离为2=2×2=5(6分)分别以D,D的方向为x轴,y轴的正方向,过点D垂直于平面ABCD的直线为z轴建立如图所示的空间直角坐标系D(7分)则D(0,0,0),B(4,2,0),C(0,2,0),P(1,0,3)所以P=(-1,2,-3),BC=(-4,0.0),更多试题,关注新浪微博《高考倒计时微博》设平面PBC的一个法向量为n=(x,y,z)取z=2,则n=(0,3,2)而平面PAB的一个法向量为DP=(1,0,3),(10分则cos(n,DP)=D(0,3,2)·(10,32nII DPI3+4×√1+3由图可知,二面角A-PB-C为钝角,所以所求的余弦值为(12分