四平三高中2022届高三质量检测(223535D)理科数学试题答案

四平三高中2022届高三质量检测(223535D)理科数学试题答案，目前我们趣对答案已经整理了四平三高中2022届高三质量检测(223535D)理科数学试题答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

1l.ABC由抛物线的光学性质可知直线PQ过焦点F(1,0),∴nx2=2=1,选项A正确;由题意可得,点P的坐标为(,1),点Q的坐标为(4,-,∴=3,选项B正确:由抛物线的定义可知,PQ=n+n+p=1+4+2=2,选项C正确;∵h与h平行,∴h与b2之间的距离d=1y-y2|=5,选项D错误

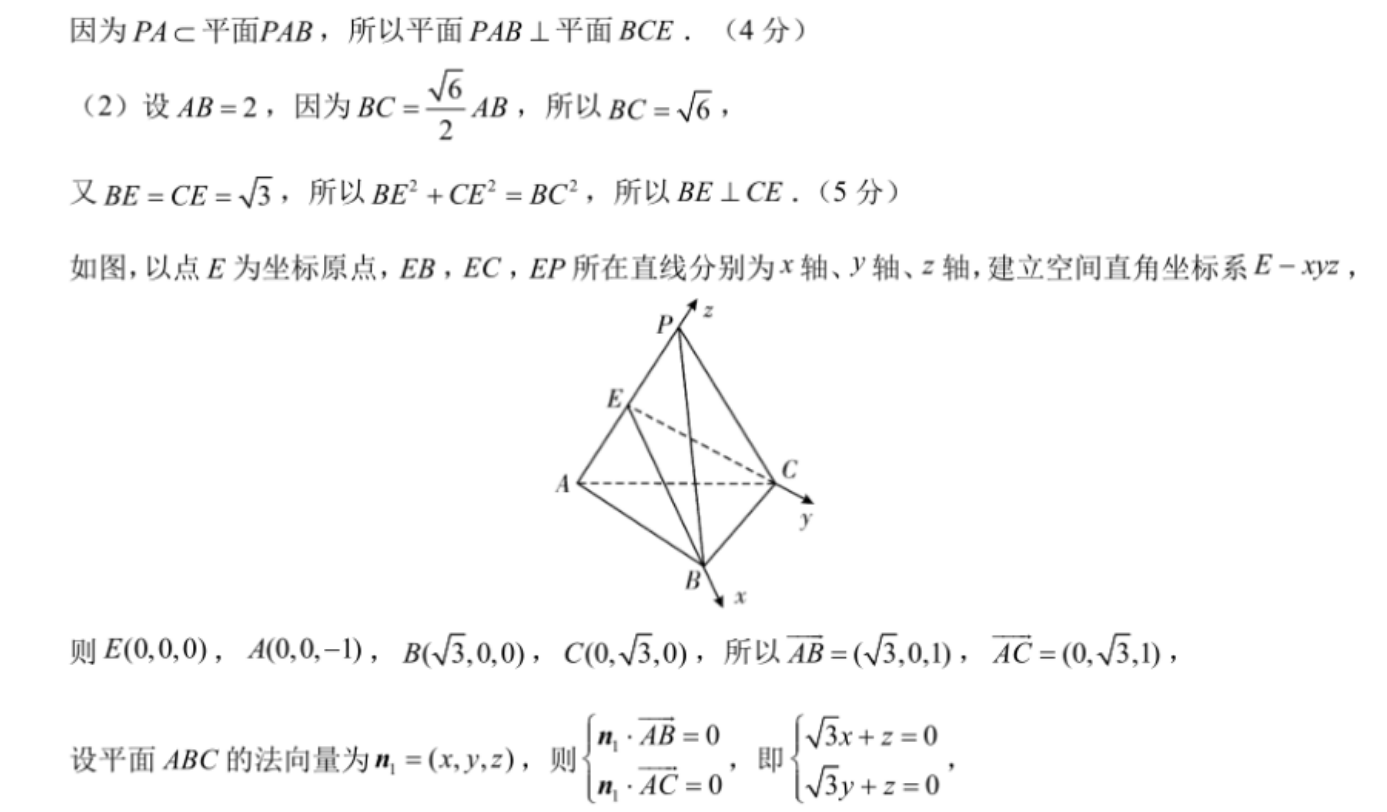
19.(12分)【解析】(1)因为PB=AB,E是PA的中点,所以PA⊥BE,(1分)同理可得PA⊥CE,(2分)因为BE∩CE=E,所以PA⊥平面BCE.(3分)因为PAc平面PAB,所以平面PAB⊥平面BCE.(4分)(2)设AB=2,因为BC=AB,所以BC=√6,2又BE=CE=√3,所以BE2+CE2=BC2,所以BE⊥CE.(5分)如图,以点E为坐标原点,EB,EC,EP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系E-xz,则E(0,0,0),A(00,-1),B(√3,0,0),C0、√3,0),所以AB=(3,0,1),AC=(0.√3,1),n1·AB=0x+z=0设平面ABC的法向量为n1=(x,y,z),则即n,·AC=0y+z=0令x=√3,可得z=-3,y=√3,所以平面ABC的一个法向量为n=(3,√3,-3),(8分)易知CE⊥平面ABE,所以平面ABE的一个法向量为n2=(0,1,0),(10分)所以 cos(n,n2)=√3√5n1|1n2|√15×1,(11分)所以二面角E-AB-C的正弦值为2y.(12分