衡水金卷先享题·2022届高三二轮复习专题卷 理数(二)2答案

衡水金卷先享题·2022届高三二轮复习专题卷 理数(二)2答案，目前我们趣对答案已经整理了衡水金卷先享题·2022届高三二轮复习专题卷 理数(二)2答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

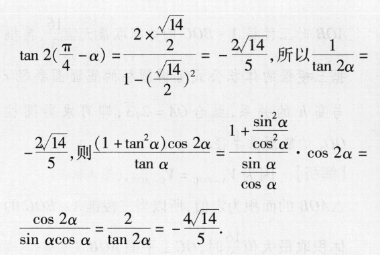
7.B【解题思路】首先由题意得sin(牙-a)-咨再将条件m(子-)-号民开，支形，通过切化弦化简I+an0,利用诱导公式及二倍角公式tan o得cos2a=214即可求得结果【解析】解法一因为角α为第四象限角，m(好-)=号所以a(-)由cos(4-a)=22(cos a+a)=号得sa+3,所以2 sin c=-52sin a,则+amatan a1+sin'acosa1sin asin acos a5,又cos2a=cos an(号-2a）=2sn(牙-a)cos(号-w)=29,(诱导公式、二倍角公式的应用)所以1+an2m)cos2a--18×24_-44tan a595解法二因为角a为第四象限角，cos(-a）=冬所以sn(牙-a)-m(-a)-2,得2×号2g所以m2好-0121+sin a-3则1+22=cos"a·c0s2a=sin acos acos 2a=244sin acos atan 2a5

10.B【解题思路】先根据已知得到OC⊥平面A0B时三棱锥A-B0C的体积取最大值5，再根据三棱锥的体积公式可得圆柱的底面圆半径π与高h的关系，结合OA=2W3,即可求得圆柱001的底面圆半径.【解析】因为VA-oc=Vc-AoB,(等体积法)△AOB的面积为定值，所以当三棱锥A-BOC的体积取最大值时，0C⊥平面A0B.(方法：三被锥的某个面的面积固定，求该三棱锥体积的最大值可转化为求高的最大值)设圆柱底面圆的半径为，高为点，则兮×)×2h×r=5,即Fh=16,又户+R=0m=12,所以h=2,r=22.故选B.