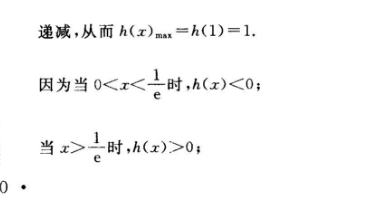衡中文化2022年普通高等学校招生全国统一考试·调研卷 甲卷(五)5文科数学试题答案,目前我们趣对答案已经整理了衡中文化2022年普通高等学校招生全国统一考试·调研卷 甲卷(五)5文科数学试题答案的各科答案和试卷,更多试卷答案请关注本趣对答案。


19解:(1)因为a,b,m均为正实数欲证bbaT an只要证明a(b+m)

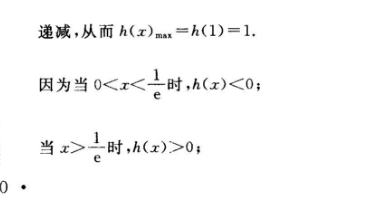



21.解:(1)由题意,求得f(x)=nx+1-ax,因为f(x)有两个不同的极值点,则f(x)有两个不同的零点,(2分)令f(x)=0,则lnx+1-ax=0,即a=hx+1设h(x)=hx+则直线y=a与函数y=h(x)的图象有两个不同的交点(3分)因为h(x)(In x+1) In x由h(x)>0,得0
1所以h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,从而h(x)ms=h(1)=1.递减,从而h(x)mn=h(1)=1.因为当0
一时,h(x)>0;当x→+∞时,h(x)→0,所以a的取值范围是(0,1)(5分)(2)因为x1,x2为f(x)的两个极值点则x1,x2为直线y=a与曲线y=h(x)的两个交点的横坐标由(1)可知,1
x2时,a,即f(x)当x1
0则∫(x)在(0,x),(x2,+∞)上单调递减,在(x1,x2)上单调递增,(7分)所以f(x)的极小值点为x1,极大值点为x2当0
1,则g(x)=xhnx-ax2-<0,所以g(x)在区间(0,1]内无零点因为g(x2)=x2lnx2-7x2-=x2lnx2-(In x2+1)Iy xz x2(Ina=h(x2),则①当lnx2>2,即x2>e2时,g(x2)>0又0
1所以g(e)=e(ne-a·e是22(1-e)-2<0此时g(x)在(1,x2)和(x2,+∞)内各有1个零点,且a
h(e2)=综上分析,当0