衡水金卷 先享版 调研卷 2022年普通高等学校招生全国统一考试模拟试题文综(二) 答答案

衡水金卷 先享版 调研卷 2022年普通高等学校招生全国统一考试模拟试题文综(二) 答答案，目前我们已经整理了衡水金卷 先享版 调研卷 2022年普通高等学校招生全国统一考试模拟试题文综(二) 答答案的各科答案和试卷，更多试卷答案请关注本答案网。

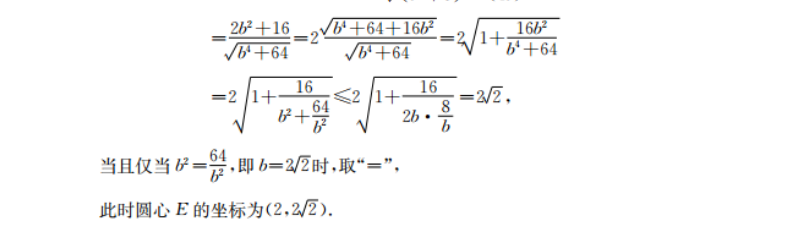
20解析:(1)如图,设点P在抛物线准线直线x=-是上的射影为M,由抛物线的定义可得I PM =PFI则当NMP三点共线时,PN+PF取最小值MM=3-(-2)=4,解得p=2所以抛物线C的方程为y2=4x.(2)设圆心到了)圆E的方程为(x-2)2+(y-b)2化简得x2+y2-92x-2y+b2-4=0令x=0,得y2-2by+b2-4=0,即[y-(b+2)][y-(b-2)]=0所以y=b+2或y=b-2,不妨设A(0,b+2),B(0,b-2),|DA|=m,|DB|=n,则m=|DA|=√4+(b+2)2=√b+4b+8,n=|DB|=√4+(b-2)2=√b-4b+8,+1B+m=2+m2=2=4+8++4+8mnm√(b2+8)2-(4b)22b2+16。√b+64+16√b+64√b+64b4+64√b+64√b+64b4+642当且仅当矿=,即b=2时,取“=”此时圆心E的坐标为(2,2/2)

2.解析:(1)依题意,2-=12,b=2,解得a=4,所以C的直角坐标方程为2+x=1将x=Pcos0,y=psin0代入,得曲线C的极坐标方程为p2cos20+4d2sin20=16.易知直线PQ的直角坐标方程为x+3y-2/3=0,同理可得直线PQ极坐标方程为Pcos0+3in0=23(2)依题意,直线MN的参数方程为(t为参数),将此参数方程代入C的直角坐标方程中,整理得1312+8/3t-16=0,因此MN|=|t1-t2|=√(1+t2)2-41t2,将h+=-当=-19代人上式,得MN-