2022年普通高等学校招生全国统一考试·信息模拟测试卷(四)4文科数学答案

2022年普通高等学校招生全国统一考试·信息模拟测试卷(四)4文科数学答案，目前我们已经整理了2022年普通高等学校招生全国统一考试·信息模拟测试卷(四)4文科数学答案的各科答案和试卷，更多试卷答案请关注本答案网。

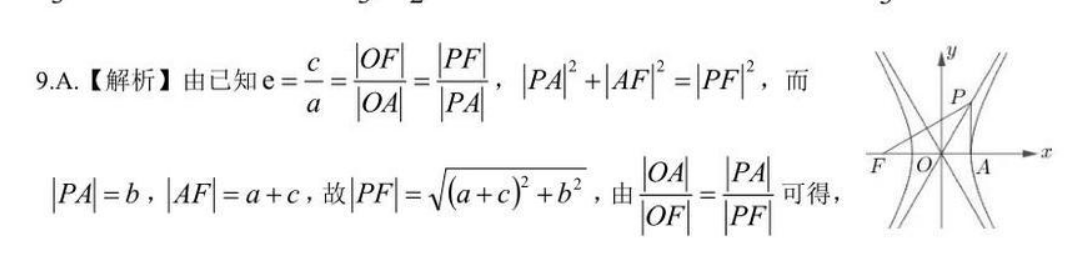
9A.【解析】由已知e=S=}pa-m面P4-6ae,放P阴-8，由8-可得，b,整理可得e=2.Va+c)+b2另解：根据题意可得点F的坐标为(-c,0),点P的坐标为(a,b),其中c=√a2+b2,所以直线PF的方程为y=bx+c),即br-a+cy+bc=0,所以坐标原点O到直a+cbc线PF的距离等于=.因为PA⊥AF,所以点O到直线PA的距离等于Vb2+(a+c)bcOA=a,由OP平分∠APF,得b2+(a+c)2=a,变形为+a+因为离心率e=>0,又=c2-d2,所以e=+&解得e=2.故选A.

22.选修4一4：坐标系与参数方程]（本小题满分10分）【解析】(I)由已知可得直线1的普通方程为√3x-y+m=0,曲线C的直角坐标方程为x2+(y-2}=4,根据点到直线的距离公式可知m-2=m-2=2,M)+P2解得m=6或m=-2,又m<0,所以m=-2..5分(II)由(I)可知直线OA的方程为x-√3y=0,而且弦OA的长度一定，要使△OPA的面积最大，只需点P到直线OA的距离最大，设P(2cosa,2+2sina),则点P到直线OAt4的距离bsa-v50inapo--2所以当eoa+）-l即a=2+keZ时，图离最大，此时点P的坐标为(1,2+V….10分