[兰州一诊]2022年兰州高三诊断考试英语答案

[兰州一诊]2022年兰州高三诊断考试英语答案，目前我们已经整理了[兰州一诊]2022年兰州高三诊断考试英语答案的各科答案和试卷，更多试卷答案请关注本答案网。

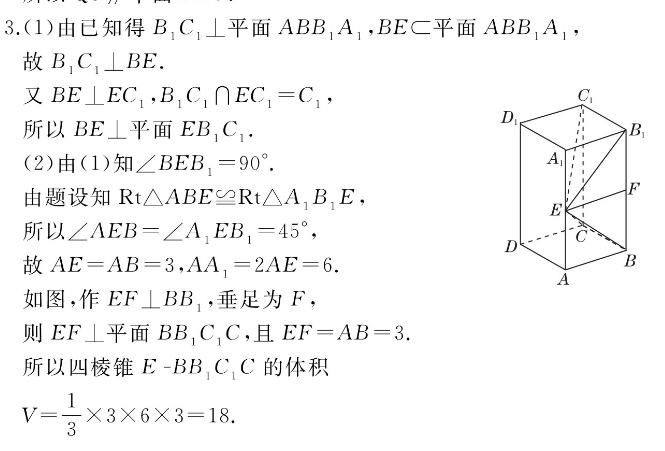
(1)由已知得BC1⊥平面ABB1A1,BEC平面ABB1A1故B,C,⊥BE又BE⊥EC1,B,C1∩EC1=所以BE⊥平面EB1CB(2)由(1)知∠BEB,=90由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=∠A,EB1=45故AE=AB=3,AA1=2AE=6如图,作EF⊥BB1,垂足为F则EF⊥平面BB1C1C,且EF=AB=3所以四棱锥E-BBCC的体积×3×6×3=18

12.(1)如图,连接OB,因为ABCD为菱形,O为菱形的中点,所以AO⊥OB因为∠BAD=60°,所以OB=AB·sin∠OAB=2sin30°=1,又因为BM且∠OBM=60°,所以在△OBM中OM2=OB2+BM2-2OB·BM·cos∠OBM2×1××cos60所以OB2=OM2+BM2,故OM⊥BM又PO⊥底面ABCD,所以PO⊥BC从而BC与平而POM内两条相交直线OM,PO都垂直所以BC⊥平面POM(2)由(1)可得,OA=AB·cos∠OAB=2·cos30°=√设PO=a,由PO⊥底面ABCD知,△POA为直角三角形故PA2=PO2+OA2又△POM也是直角三角形,故PM2=PO2+OM2=a2+连接AM,在△ABM中,AM2=AB2+BM2-2AB·BM·cos∠ABM=22+2×2××cos120°≈27由于MP⊥AP,故△APM为直角三角形,则PA2+PM2321AM2,即a2+3+a2+=,得a=。或(舍去),即PO此时S四边形ABMD=S△AOB+S△OMB12125AO·OB+-·BM·OM11×√3×1+×所以Vp-ABM3四边形ABM·PO15√3√358