鄂东南三校联考2022年秋季高三年级阶段(一)1考试(233132D)物理答案

鄂东南三校联考2022年秋季高三年级阶段(一)1考试(233132D)物理答案，目前我们已经整理了鄂东南三校联考2022年秋季高三年级阶段(一)1考试(233132D)物理答案的各科答案和试卷，更多试卷答案请关注本答案网。

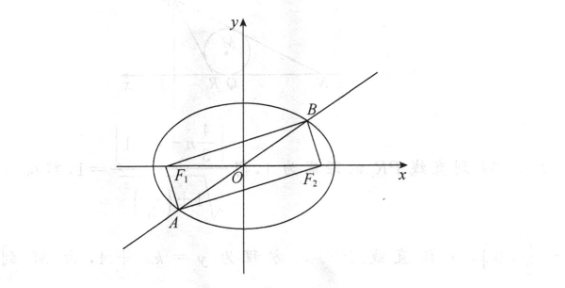
12.过原点的一条直线与椭圆子++=1(a>b>0)交于A,B两点，F:为椭圆右焦点，且AB的长度等于焦距长.若∠ABF,∈（，,则该椭圆离心率的取值范围为)c()(【答案】B【解析】如图，由题可知，AB长度等于焦距长且直线AB过原点，由椭圆的对称性可知，四边形AF2BF1是矩形，则∠AF,B=,AF,=2csin∠ABF2,lAF,l=BF,=2ccos∠ABF,又因为点A在精圆上，所以11|AF1|+|AF2|=2csin∠ABF2+2ccos∠ABF2=2a,即e=sin ZABF,+o/ABF:Esin(∠ABF+）图为∠ABF,∈（危·），即∠ABF,+∈（行，）所以Esm(∠ABF:+)∈（受，E],故evesn(2aBn+停yBFFA

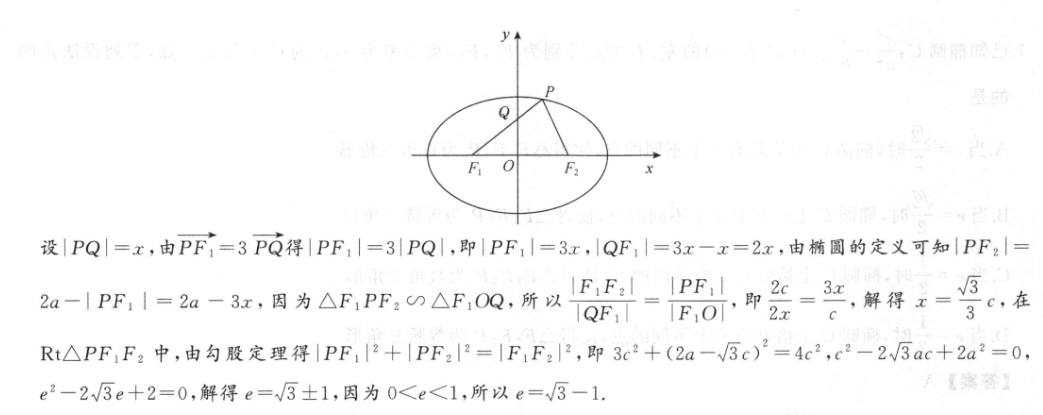
y?=1(a>b>0)的左、右焦点分别为F,F,P为椭圆上一点，且PF1⊥PF,线段PF,与y轴相交于点Q.若PF=3PQ,则椭圆的离心率为A.2-√5B.3D.W5-12【答案】D【解析】如图，F OF2设|PQ=x,由PF1=3PQ得|PF,|=3|PQ,即|PF,|=3x,QF,|=3x一x=2x,由椭圆的定义可知|PF2|=2=3虹，解得工=2a-PF,=2a-3x,周为△F,PF,0△F,0Q,所以-P,即=33c,在Rt△PF1F2中，由勾股定理得PF,I2+PF2|2=|F1F22,即3c2+(2a-√5c)2=4c2,c2-2√5ac+2a2=0,e2-2√3e+2=0,解得e=√3士1，因为0