衡水名师卷·2022-2023学年度高三分科检测提分卷·151靶向提升(老高考)英语(四)4试题 答案

衡水名师卷·2022-2023学年度高三分科检测提分卷·151靶向提升(老高考)英语(四)4试题 答案，目前我们已经整理了衡水名师卷·2022-2023学年度高三分科检测提分卷·151靶向提升(老高考)英语(四)4试题 答案的各科答案和试卷，更多试卷答案请关注本答案网。

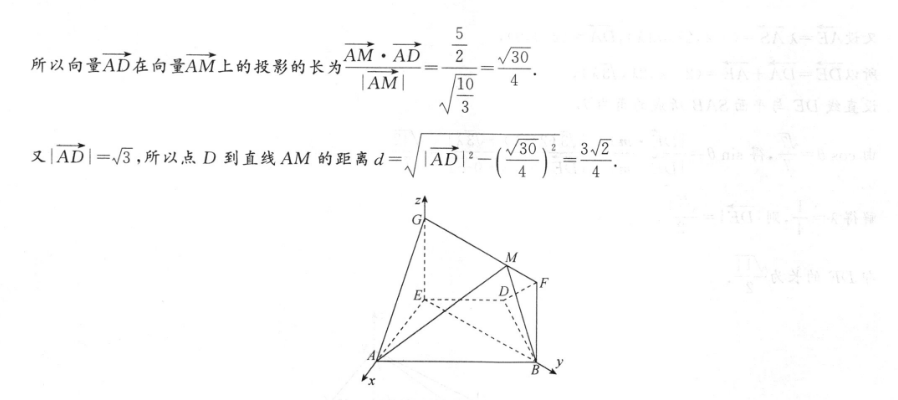
(1)证明：因为EG=BF,所以EG∥BF,且EG=BF,又BF⊥BE,BF⊥BD,BE∩BD=B,BE,BDC平面ABDE,所以BF⊥平面ABDE,则EG⊥平面ABDE,又EBC平面ABDE,所以EG⊥EB.又AE=ED=DB=1,ED∥AB,所以四边形ABDE为等腰梯形，又∠EAB=60°，所以∠BDE=∠AED=120°，则∠DEB=30°，则∠AEB=90°，即AE⊥BE,又AE∩EG=E,AE,EGC平面AEG,所以BE⊥平面AEG,又BEC平面GEBF,形所以平面GEBF⊥平面AEG.(2)解：由(1)知，EA,EB,EG两两垂直，以E为原点，射线EA,EB,EG分别为x,y,之轴的非负半轴建立空间直角坐标系Exyz,如图，因为AE=ED=DB=BF=1,四边形GEBF是矩形，所以G=BE-5,pA100.B050.G00.D(-g.o）形粉McG=-2M,得Mo,25,到-(129ad-(9M.AD5历所以向量AD在向量AM上的投影的长为IAMI/104又Ai=5,所以点D到直线AM的距离d=ò-(0-MEDAB

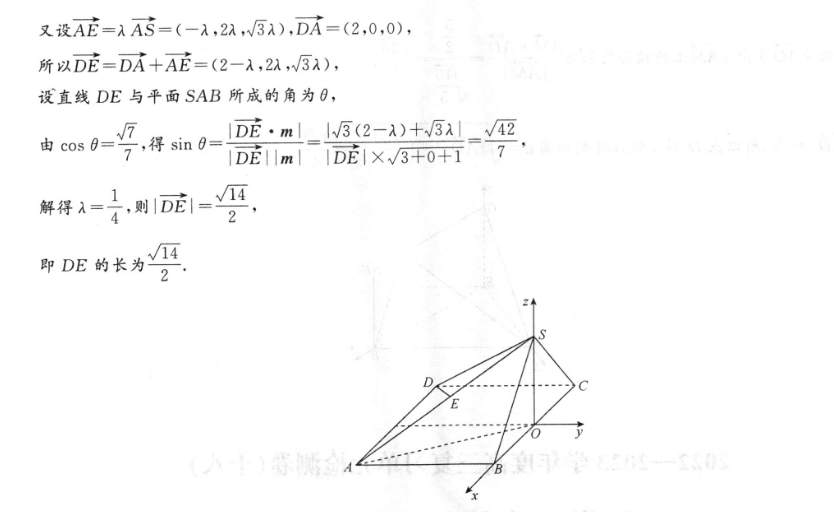
解：(1)在正方形ABCD中，BC∥AD,则异面直线BC与SD所成角即AD与SD所成角，如图，取BC的中点O,连接SO,因为平面SBC⊥平面ABCD,平面SBC∩平面ABCD=BC,SO⊥BC,SOC平面SBC,所以SO⊥平面ABCD.设AB=a,则AD=a,S0=2a,则AS=DS=A0+S0-a++-=√2a,所以coS∠ADS=DA+DS2-AS2、√22DA·DS2XaX√2a4则异面直线BC与SD所成角的余弦值为4(2)因为SO⊥平面ABCD,以O为坐标原，点，OS,OB所在直线分别为之，x轴，过O在平面ABCD内作BC的垂线为y轴，建立如图所示的空间直角坐标系Oxyz,由AB=2,得A(1,-2,0),B(1,0,0),S(0,0,5),D(-1,-2,0),AB=(0,2,0),A5=(-1,2N3),设平面SAB的一个法向量为m=(x,y,z),m·AB=0,2y=0,由即m·A5=0,-x+2y+3zx=0,令之=1，得m=(3,0,1).又设AE=AAS=(-A,2入，W3A),DA=(2,0,0),所以DE=DA+AE=(2-A,2x,√3λ)，设直线DE与平面SAB所成的角为0，由c0s0=1DE·m|5(2-λ)十3λ_√42DE1Im|IDE1X√3+0+I7解得入-则成=。即DE的长为2