金太阳2022届山东高三阶段质量检测(22-12-280C)数学答案

金太阳2022届山东高三阶段质量检测(22-12-280C)数学答案，目前我们趣对答案已经整理了金太阳2022届山东高三阶段质量检测(22-12-280C)数学答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

20.解:(1)f(x出题意得f(2)=2-ln2+4=1-1n2,则a=2(4分(2)不等式可化为a<2(11nx)x (1+In x)r*In.设g(x)=x-lnx-2,当x>1时则g(x)在区间(1,+∞)上单调递增又g(3)=1-ln3<0,g(4)=2-ln4>0,则g(x)在区间(3,4)上存在唯一零点x0,满足g(x)=x-lnxo-2=则当x∈(1,x)时,h(x)单调递减,当x∈(xo,+∞)时,h(x)单调递增,则h(x)≥h(xc (Itin oT又因为x-1nx。-2=0,则h(x2)=2(x-1)=x,因为x∈(3,4),则a

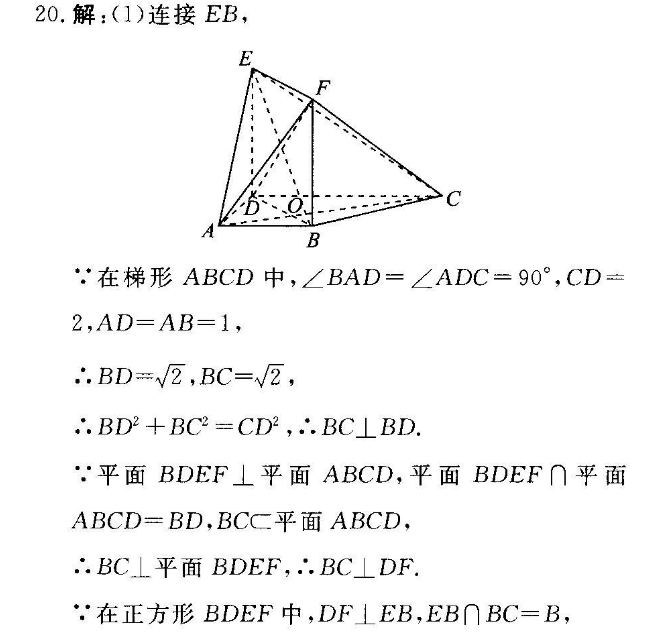
20.解:(1)连接EB,务:B∵在梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,BD=√2,BC∴BD2+BC2=CD2,∴BC⊥BD平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,BCC平面ABCD,∴BC⊥平面BDEF,∴BC⊥DF∵在正方形BDEF中,DF⊥EB,EB∩BC=B∴DF⊥平面BCE∵CEC平面BCE,∴DF⊥CE(6分)(2)在AE上存在点G,当AG=1时,使得平面OBGGE 2∥平面EFC证明如下:∵AB∥DC,AB=1,DC=2,Ao 1又GE=2…OG∥CE,又OG≠平面EFC,CEC平面EFC,∴OG∥平面EFCEF∥OB,EFC平面EFC,OB￠平面EFC,∴OB∥平面EFC∵OB∩OG=0,∴∵平面OBG∥平面EFC.(12分)