衡中文化2022年普通高等学校招生全国统一考试·调研卷(一)1理科数学试题答案

衡中文化2022年普通高等学校招生全国统一考试·调研卷(一)1理科数学试题答案，目前我们趣对答案已经整理了衡中文化2022年普通高等学校招生全国统一考试·调研卷(一)1理科数学试题答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

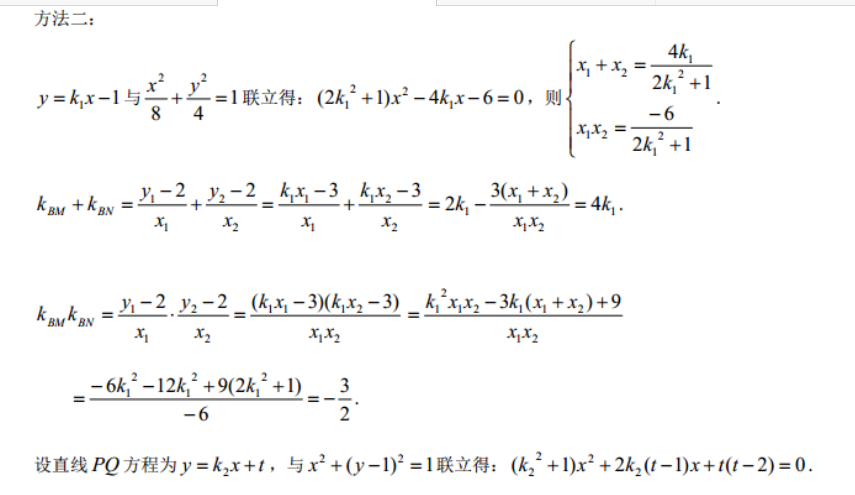
22解(1)由题意,b-(-1)3,解得b=2设椭圆半焦距为c,则2’即1、b2解得a8∴椭圆的标准方程为(2)设M(x,y),N(x2,y2),P(xP,yP),Q(x,y),直线MN方程为y=kx-1方法直线BM方程为y=-2x+2,与x2+(y-1)2=1联立得(x2+(y1-2)2)x2+2x1(y1-2)x=01(y1由x≠0,解得xx2+(~32又+2=1,即x2=8-2y12,代入上式,得xP=2(4-y)+(1-2)2y1+6y1-216y+62x即点P(同理,点Q(V,+yIy2+6y2(4、、l6Pye+164163<+168(y1-y2)xp-oy2-x2y1+6x1=6x2y1+6y2+6将y=k1x1-1,y2=k1x2-1代入上式得k2=8k1(x1-x2)x1(kx2-1)-x2(kx一1)+6(x1-x2)5(x-x2)k2==k1,∴元12分方法二:x1+x2y=k1x-1与1联立得:(2k12+1)x2-4k1x-6=0,则rE22k,+yI工-3+42-3=2-3(x+x2)xI2kk=-2.-2=(x-3)kx2-3)_Axx2-3k(x+x2)+9xt26k12-12k2+9(2k2+1)〓一设直线PQ方程为y=k2x+1,与x2+(y-1)2=1联立得:(k2+1)x2+2k2(t-l)x+t(t-2)=0re+2(k2+1r(t-2)yyok2x2+1-2,k2o+1-2=2k+(t-2)(xp+x)Xpo(t-2)(t-1)2k2knkm=-2.-2(k2x+1-2)kx+1-2)2xpx0+k2(-2)x+x)+(-2)k,2(t-2)-2k2(-2)(1-1)+(k2+1)(-2)2k,2t-2k,(-1)+(k,2+1t-2)t-2(t-2)4解得kkgu kgn=kgpkBg3 t12分

9.(12分)解:BDAD(1)在三角形ABD中,由正弦定理得:sin∠ BAD sin∠DBAAD·sin∠BAD6sin30°3得:sin∠DBA=,cos∠DBA=±、|l-(BD∵∠DBA<∠ABC,∴cos∠DBA>cos135°√2故cos∠DBA=-一不符合题意,∴cos∠DBA=6分(2)coS∠DBC=cos(∠ABC-∠DBA)=-2.4√2322510在三角形BCD中,CD=√BC2+BD2-2BC.BD,cos∠DBC=18+25+23√2510∴CD=7…12分