2022届普通高校招生考试仿真模拟卷(五)5理科数学Y答案

2022届普通高校招生考试仿真模拟卷(五)5理科数学Y答案，目前我们趣对答案已经整理了2022届普通高校招生考试仿真模拟卷(五)5理科数学Y答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

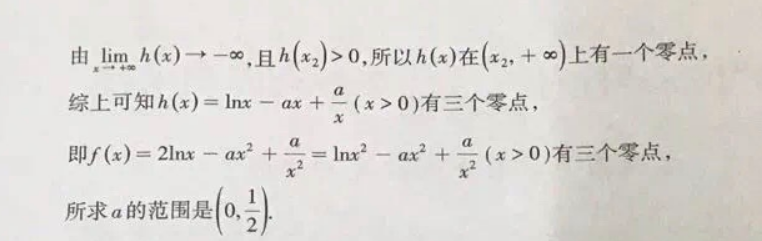
1.(本小题满分12分)解:(1)证明:f(2=2-令211+==g(t2g()=2-62-2=2(21-1-62<0g)在(02上单调速减(0(2-2m2-4+4=4--2120所以原命题成立分(2)由f(x)=2mx-ax2+=lmx2-ax2+2(x>0)有三个零点可得h(x)=mnx-ax+-(x>0)有三个零点,h(x)=-ax+x-ax2①当a≤0时,h'(x)>0恒成立,可得h(x)至多有一个零点,不符合题意;②当时,h'(x)≤0恒成立,可得h(x)至多有一个零点,不符合题意8分③当0 0得两个零点为x1x不妨设0 0;x∈(x2+叫)时h(x)<0观察可得h(1)=0,且x1<1 0;h()单调递增所以有)0)≤(3,即6()<0(xx∈()时,h(x)<0.A(x)单调递减,x∈(2,+)时h()<0,()单调递减……10分1)知42=0且小0所以M)在上有一个零点由mh(x)→一∞,且A(x3)>0,所以A()在(x2+叫)上有一个零点,综上可知h(x)=hnx-ax+(x>0)有三个零点,即f(x)=2hnx-ax2+=lnx2-ax2+a(x>0)有三个零点,所求a的范围是02

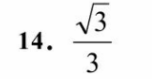
1433