2022届金太阳山西高三1月联考(22-12-242C)理科数学试题答案

2022届金太阳山西高三1月联考(22-12-242C)理科数学试题答案，目前我们趣对答案已经整理了2022届金太阳山西高三1月联考(22-12-242C)理科数学试题答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

22.解:(1)由题可知,AB=4,PO:=1设正四棱锥P-A1BCD1的侧面高为h,则满足PG+(3B)2将AB=4,PO1=1代入上式可得,h=√5,则正四棱锥PA1B1C1D1的侧面积为Sm=4×2√5×4=85,正四棱柱ABCD-A1B1CD1的底面面积为S底=4:×4=16,正四棱柱ABCD-A1B1C1D1的侧面积为S刻=4×2×4=32,则该仓库的表面积为48+8√5m2.(6分)(2)设A1B1=a,PO=h,则0 0,V是单调递增函数;当

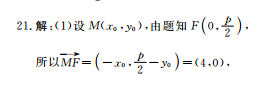
21解:(1)设M(x,y),由题知F(0,5),所以M=(-x0,-y)=(4,0),所以即1=f代入x2=2py(p>0)中,得16=p2解得p=4,所以抛物线C的方程为x2=8y.(4分)(2)由题意知,直线AB的斜率存在,设其方程为y=kx+b(b>0),y=kx+b由整理得x2-8kx-8b=0,△>08则x1+x2=8k,x1x2=-8b,所以y+y2=k(x1+x2)+2b=8k2+2b,设AB的中点为Q,则点Q的坐标为(4k,4k2+b),(7分)由条件设切线的方程为y=kx+t,=kx+t则整理得x2-8kx-8t=0x2=8因为直线与抛物线相切,所以△=64k2+32t=0,所以t=-2k2,所以x2-8kx+16k2=0,则x=4k,所以y=2k2,即切点N的坐标为(4k,2k2),(9分)所以NQ⊥x轴,则|NQ|=(4k2+b)-2k2=2k2+b,又|x2-x1|=3,且(x2-x1)2=(x2+x1)2-4x1x2=64k2+32b,所以2k2+b=9,则S△AN=|NQ|·|x:-x1|=(2k2+b)·|x2即△ABN的面积为定值,且定值为6(12分)